ANNOUNCEMENTS
MTH 679 — Spring 2016
- 6/1/16
-
Lecture notes covering "conformalization", as discussed in class, are
available
here.
- 5/27/16
-
A standard reference on the octonions is the article by John Baez, which is
available here.
- 5/26/16
-
Lecture notes covering the counting arguments for the magic squares, as
discussed in class, are available
here.
-
These notes include the tables passed out in class, a corrected version of
which can be found
here.
- 5/25/16
-
You are encouraged to consider submitting missing homework assignments, if
any, by next Wednesday, 6/1/16.
-
There are some students for whom this could
affect their course grade.
Resubmitting an assignment on which you received a poor score is also permitted.
- 5/20/16
-
A Mathematica package for multiplying octonions is available
here.
-
The minimal documentation fails to mention that the octonionic units can be
entered as one,i,j,k,kl,jl,il,l.
-
This version of the package is old, but appears to still work; if you have
difficulty, please let me know.
- 5/17/16
-
Tomorrow's office hour will be shifted forward 30 minutes, and will run from
1 PM to 3 PM.
- 5/13/16
-
Strange but true: The 13th of the month is more likely to be a Friday than
any other day of the week!
-
Give up? Further information is available here.
- 5/12/16
-
My office hours tomorrow will be interrupted by a 2 PM commitment. I will
be in my office from 1:30–2 PM and again from 3–3:30 PM.
- 5/11/16
-
As alluded to in class today, you can find a fascinating and reasonably
accessible paper on the applications of $G_2$ to rolling balls
here.
- 5/8/16
-
As promised, lecture notes describing the details of the classification of
roots and Dynkin diagrams are available
here.
-
You may also wish to consult the presentations in Fulton and Harris or
Erdmann and Wildon; see the book list.
-
The previous notes on roots have also been slightly edited; the updated
version is available
here.
-
The full set of notes is now also available in wiki format
here.
- 5/3/16
-
The next installment of lecture notes, discussing roots, is available
here.
- 4/29/16
-
This week's homework contained an error;
a corrected copy is available here.
-
$V$ is a collection of vectors in $\RR^n$, but not a vector space. It
is however important that the given assertion holds for all pairs of elements
in $V$. (HINT: The assertion is not symmetric!)
- 4/28/16
-
The next installment of lecture notes, covering $\su(3)$ and the
representations of $\su(2)$, is available
here.
-
Notes discussing the classification of Lie algebras should be available
sometime next week.
- 4/27/16
-
Tomorrow's office hour will be shifted forward 30 minutes, and will run from
1 PM to 3 PM.
- 4/25/16
-
Further information about the $2\times2$ magic square of Lie algebras can be
found in
§15.2
of GO.
- 4/23/16
-
This week's homework has been slightly reworded; a
corrected copy is available here.
-
Problem 1(f) no longer asks you to rescale your basis, and Problem 1(g) asks
you not to use your rescaled basis.
- 4/22/16
-
I unfortunately had to stop just short of a nice punchline today, so here it
is.
-
We have the following basis elements for
$\sl(2,\RR)\cong\su(2,\CC')\cong\so(2,1)$, a real form of $\su(2)$:
\[
\sigma_0=\frac12\sigma_z,
\quad
\sigma_\pm=\frac12(\sigma_x\mp s_y)=\frac12(\sigma_x\pm i\sigma_y),
\]
with commutation relations
\[
[\sigma_0,\sigma_\pm]=\pm\sigma_\pm,
\quad
[\sigma_+,\sigma_-]=2\sigma_0.
\]
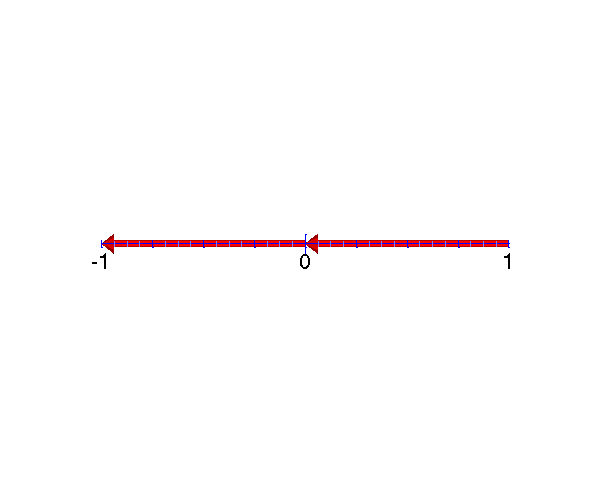 We can thus represent $\sl(2,\RR)$ graphically as the points $0,\pm1\in\RR$,
representing $\sigma_z$ acting on itself and $\sigma_\pm$, respectively,
connected by oriented arrows representing the action of $\sigma_\pm$, as shown
at the right. This diagram fully captures the algebraic description
$\sl(2,\RR)$ acting on itself, the so-called adjoint representation of
$\sl(2,\RR)$.
We can thus represent $\sl(2,\RR)$ graphically as the points $0,\pm1\in\RR$,
representing $\sigma_z$ acting on itself and $\sigma_\pm$, respectively,
connected by oriented arrows representing the action of $\sigma_\pm$, as shown
at the right. This diagram fully captures the algebraic description
$\sl(2,\RR)$ acting on itself, the so-called adjoint representation of
$\sl(2,\RR)$.
-
The technique described here is more commonly applied to the
complexified Lie algebra $\su(2)\otimes\CC$; the figure is called the
root diagram of $\su(2)$.
- 4/21/16
-
The next installment of lecture notes, covering definitions and
$\SU(2,\CC'\otimes\CC)$, is available here.
- 4/20/16
-
The counting argument I made in class today was incomplete.
-
-
In any special unitary group, we have $M^\dagger M=1$ and $|\det M|=1$.
-
Consider first $\SU(2,\CC)$. A $2\times2$ complex matrix has 4 complex, and
hence 8 real, parameters. $|\det M|=1$ is a single complex constraint, and
$M^\dagger M=1$ is 2 real constraints plus 1 complex constraints. This
argument appears to yield 6 real constraints, which would leave only 2 free
parameters.
-
However, $M^\dagger M=1$ already implies that $|\det M|=1$! Thus, this
constraint has been double-counted, and we conclude that $\SU(2,\CC)$ is
3-dimensional.
-
Exactly the same counting argument holds for $\SU(2,\CC')$.
-
Now consider $\SU(2,\CC'\otimes\CC)$. A $2\times2$ matrix over
$\CC'\otimes\CC$ has 16 real parameters. $\det M=1$ now provides 4
constraints. The off-diagonal term in $M^\dagger M=1$ also yields 4 real
constraints. So far so good. But the diagonal terms in $M^\dagger M=1$ are
no longer real! They provide 4 real constraints, rather than the expected 2.
We thus appear to have 12 constraints, leaving 4 free parameters.
-
The resolution is the same as before, with careful counting. $M^\dagger M=1$
still implies that $(\bar{\det M})(\det M)=1$, but this is now 2 conditions,
rather than one. These 2 constraints have been double-counted, and we
conclude that $\SU(2,\CC'\otimes\CC)$ is 6-dimensional.
-
The key difference between these two cases is that the product $x\bar{x}$ in
$\CC'\otimes\CC$ is not real, but merely Hermitian; $\CC'\otimes\CC$ is
not a normed algebra. The counting may be easier to see using the Lie algebras
$\su(2,\CC)$ and $\su(2,\CC'\otimes\CC)$, using the conditions $A^\dagger=-A$
and $\tr(A)=0$.
- 4/14/16
-
The next installment of lecture notes, covering $\SO(3,1)$, is available
here.
- 4/13/16
-
As discussed in class today, I expect to be in my office Monday afternoons
from roughly 1:30–3:30 PM.
- 4/8/16
-
The next installment of lecture notes, covering $\SU(2)$, is available
here.
-
The Hopf bundle, and the introduction to division algebras, are covered
in GO; separate lecture notes will not be generated.
- 4/6/16
-
Not surprisingly, I made the wrong choice when fixing the signs in the
matrices $S_m$ today in class. I will henceforth switch the signs to those
used in
§7.3
of GO.
-
As mentioned in class, changing the sign of (all) the commutators is
equivalent to replacing each group element by its inverse, that is, to
rotating in the opposite direction. The (local) identification of $\SU(2)$
with $\SO(3)$ is therefore more natural if the signs of the commutators
match.
(This is in fact a good argument for having the scale match as well, that is,
for eliminating the factor of 2.)
- 4/4/16
-
The next installment of lecture notes, covering $\SO(3)$, is available
here.
- 3/31/16
-
The first installment of lecture notes, covering $\SO(2)$, is available
here.
-
Please feel free to send me comments and questions —
and above all corrections!
- 3/30/16
-
The vocabulary list from today's class can be found
here.
This list will be updated throughout the term.
-
You should make an effort to look up unfamiliar words on this list, and/or
come and discuss them with me.
-
You are encouraged to work out the explicit formula for the general element of
$\SO(3)$ in terms of Euler angles. Is there a simple formula for the product
of two such elements?
-
Further discussion can be found on
Wikipedia.
- 2/9/16
-
The slides from my
talk
today in the
Algebra/Number Theory Seminar
can be found
here.
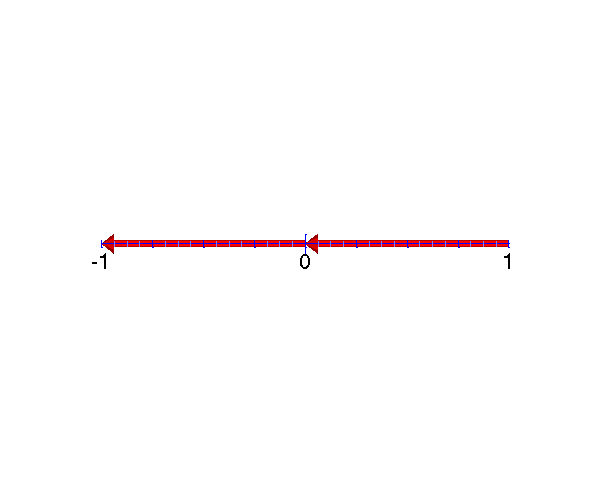 We can thus represent $\sl(2,\RR)$ graphically as the points $0,\pm1\in\RR$,
representing $\sigma_z$ acting on itself and $\sigma_\pm$, respectively,
connected by oriented arrows representing the action of $\sigma_\pm$, as shown
at the right. This diagram fully captures the algebraic description
$\sl(2,\RR)$ acting on itself, the so-called adjoint representation of
$\sl(2,\RR)$.
We can thus represent $\sl(2,\RR)$ graphically as the points $0,\pm1\in\RR$,
representing $\sigma_z$ acting on itself and $\sigma_\pm$, respectively,
connected by oriented arrows representing the action of $\sigma_\pm$, as shown
at the right. This diagram fully captures the algebraic description
$\sl(2,\RR)$ acting on itself, the so-called adjoint representation of
$\sl(2,\RR)$.