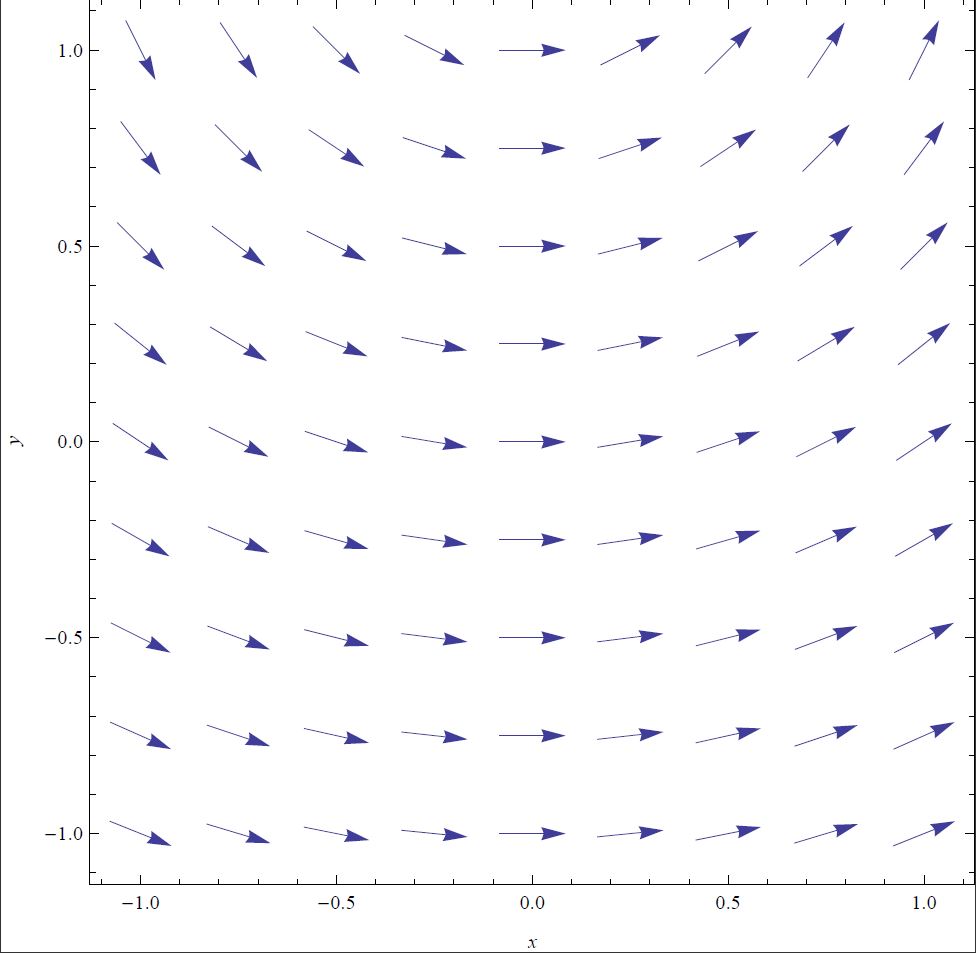
Understanding both difference (how far apart two values are at one time) and change (how far apart the value of a single parameter is at two different times) is necessary for understanding derivatives.
One can view $\frac{df}{dx}$ as approximately given by a fraction where $df$ is a small change in $f$ and $dx$ is a small change in $x$.
Technically, the derivative is a ratio of small changes in the limit that the change in the denominator goes to zero: $\frac{df}{dx}=\lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}$
One of Zandieh's process-object layers for derivatives is that derivatives are functions. This means that the value of a derivative depends on where in the domain of the function one is looking. The derivative of a function is itself a function, with the same domain as the original function. Both the (derivative) function and the value of the derivative at a point are commonly referred to as "the derivative."
For an $n-$dimensional function $f$, the gradient of $f$ at a point is an $n-$dimensional vector
The magnitude of the gradient is the value of the slope in the direction of greatest increase
The Master Formula states that a small change in a function $df$ is the dot product of the gradient of the function with a small step $d \vec r$ through the domain of the function: \[df = \vec \nabla f \cdot d \vec r.\] In order to maximize the change in $f$ one must maximize this dot product, which happens when the small step $d \vec r$ is parallel to the gradient. Or, turning this statement around, the gradient points in the direction in which the function is increasing the most.
$d \vec r$ represents a small displacement vector (i.e., it points along the direction of a step with a magnitude equal to the length of that step).