Prerequisite concepts
The magnitude of the gradient is the value of the slope in the direction of greatest increase
The Master Formula states that a small change in a function $df$ is the dot product of the gradient of the function with a small step $d \vec r$ through the domain of the function: \[df = \vec \nabla f \cdot d \vec r.\] In order to maximize the change in $f$ one must maximize this dot product, which happens when the small step $d \vec r$ is parallel to the gradient. Or, turning this statement around, the gradient points in the direction in which the function is increasing the most.
Visualizing Gradient

Building a geometric understanding of the gradient can be challenging for students, particularly in physics classrooms when their only prior exposure to the gradient is in mathematics courses. This activity is a follow-up to Acting out the Gradient, in which students use Mathematica to calculate and visualize the gradient for different representations of scalar fields. Students explicitly compare and contrast these different representations, in particular identifying that the gradient is always perpendicular to constant surfaces.
Representations used
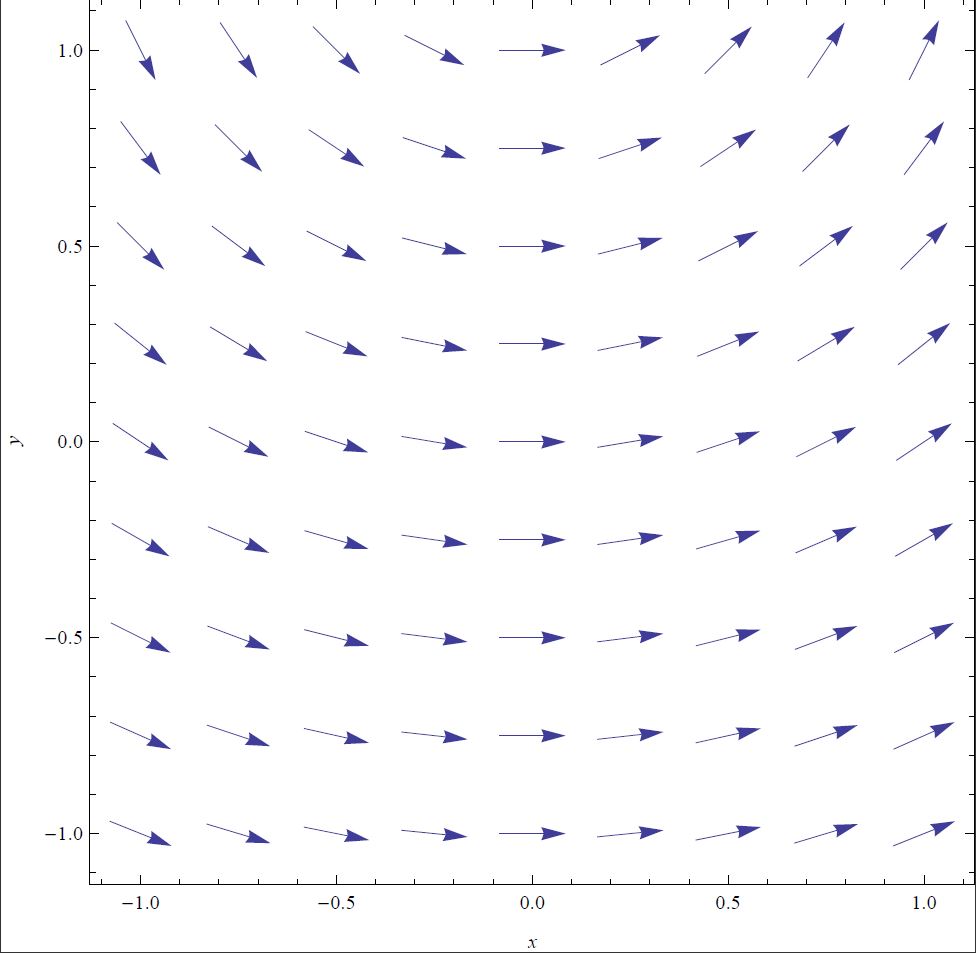
Concepts taught
The gradient of an $n$ dimensional function is $n$ dimensional. This is not to be confused with the gradient having the same physical dimensions (e.g., Newtons) as the original function.
The magnitude and direction of the gradient depends on the behavior of the function infinitesimally near the point of interest. One implication of this is that the gradient does not point in the direction of maxima a finite distance away (except sometimes accidentally), but rather in the direction of steepest slope at the point of interest.
As the gradient lies along the direction of greatest change for a function, and contour lines lie along the direction of no change, these two objects (the gradient and contour lines) are perpendicular.