One can view $\frac{df}{dx}$ as approximately given by a fraction where $df$ is a small change in $f$ and $dx$ is a small change in $x$.
Conceptually, a derivative can be thought of as how much one value changes as another value changes. FIXME: Representations
$df=\vec \nabla f \cdot d \vec r$
The derivative of a constant is always zero. This can be understood by thinking of 'The derivative is a ratio of small changes,' as the amount by which a constant changes is zero.
FIXME
In other words, $\frac{dy}{dx} = \frac{1}{\frac{dx}{dy}}$. Note that this concept is challenging to express in Newton's notation, but arises naturally if implicit differentiation is covered.
While it is relatively easy to imagine very, very small changes in physical values, there are often experimental limits on how small of a change can be measured. When designing and conducting experiments, there is a tension between these experimental limitations and normative representations of functions as smooth lines or
Technically, the derivative is a ratio of small changes in the limit that the change in the denominator goes to zero: $\frac{df}{dx}=\lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}$
Taking derivatives of the same function with respect to different variables will produce different results. In physics, these different results might have different dimensions and thus the derivative can have wildly different physical interpretations based off of "'with respect to' what".
One typical notation used for derivatives is Leibniz notation ($e.g.,$ $df/dx$). Physicists often think of the $df$ and $dx$ as distinct quantities (``differentials'') that can be measured, calculated, and manipulated independent of one another. In particular, a differential can be thought of as the (small) change in a quantity when a small change is made to a physical system. A differential can also be thought of as the difference between the values of a quantity between two different (nearby) physical states. This line of thinking is also valuable for thinking about integration in physical situations.
FIXME: Add for Contours: "The magnitude of a partial derivative is proportional to the density of contour lines along the path of the partial derivative."[]FIXME: Add for Surfaces: "The magnitude of a partial derivative is the slope of the surface along the path of the partial derivative."[]FIXME: Add current concept: "All partial derivatives can be found as a slope of a tangent plane" and change to "The Magnitude of a partial derivative a slope of the tangent plane in the direction of the partial derivative FIXME: Direction Language?"
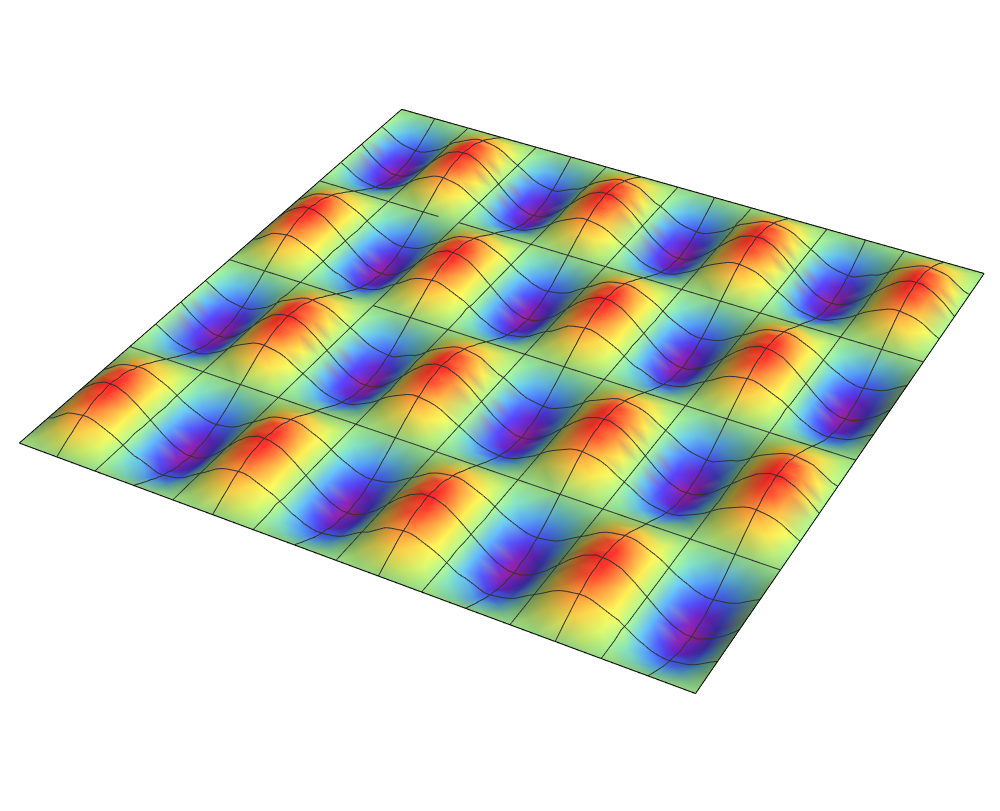

For a smooth, two dimensional function, a partial derivative can be found at any point and in any direction.
FIXME
$d \vec r$ represents a small displacement vector (i.e., it points along the direction of a step with a magnitude equal to the length of that step).
For an $n-$dimensional function $f$, the gradient of $f$ at a point is an $n-$dimensional vector
FIXME: Tangent to what path? How is this useful?
FIXME: What's the point of this concept?

The Master Formula states that a small change in a function $df$ is the dot product of the gradient of the function with a small step $d \vec r$ through the domain of the function: \[df = \vec \nabla f \cdot d \vec r.\] In order to maximize the change in $f$ one must maximize this dot product, which happens when the small step $d \vec r$ is parallel to the gradient. Or, turning this statement around, the gradient points in the direction in which the function is increasing the most.
FIXME
$df$ can be viewed as a small chunk of $f$. When combined with 'The derivative is a ratio of small changes', it's easy to relate differentials to derivatives.
The magnitude of the gradient is the value of the slope in the direction of greatest increase
No matter how complicated a multivariable function is when written as an equation, the total differential of that function will be linear in the differential terms. In other words: $dF(x,y,z)=A dx + B dy + C dz.$
FIXME: Does the difference between zapping with d and taking the total differential need to be articulated?
FIXME: What? One can do algebra with differentials and reinterpret them as partial derivatives. Can treat like a variable

The value of the derivative at a point on a curve can be approximated by the slope of a line secant with the curve near that point.
Because total differentials are linear, one can find the total differential and then solve algebraically to obtain partial derivatives that might not be obtainable though differentiation.

Just as the derivative of a one-dimensional function at a point is equal to the slope of a tangent line at that point, and partial derivative of a multivariable function can be found as a slope of a tangent plane.
One of Zandieh's process-object layers for derivatives is that derivatives are functions. This means that the value of a derivative depends on where in the domain of the function one is looking. The derivative of a function is itself a function, with the same domain as the original function. Both the (derivative) function and the value of the derivative at a point are commonly referred to as "the derivative."


When taking a derivative of a multivariable function, it is possible to consider a simpler situation in which some of the variables are considered to be constant.

The partial derivative of a function is itself a function (although taking a partial derivative at a point will just give a number). This means that the value of the partial derivative at different points in the domain will, in general, be different.
FIXME

The gradient of a function (unless taken at a single point) is itself a function
The divergence of a function (unless taken at a single point) is itself a function
If $f=f(y)$ and $y=y(x), then \frac{df}{dy}=\frac{df}{dx}\frac{dx}{dy}.$
FIXME
FIXME

The value of the derivative does not depend on what is happening far away from the point at which the derivative is being evaluated: it can be determined by what is happening in the neighborhood of the point. Geometrically, the derivative (slope) of a curve at a point is not a statement about the general shape of the curve but rather about the behavior of the curve immediately around that point.
FIXME
In each coordinate system, there exists a formula for the divergance. The standard examples are: \[\begin{align}\vec\nabla\cdot\vec v &= \frac{\partial v_x}{\partial x} + \frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z} \text{ in rectangular coodinates} \\ \vec\nabla\cdot\vec v &= \frac{1}{s}\frac{\partial \left(s v_s\right)}{\partial s} + \frac{1}{s}\frac{\partial v_\phi}{\partial \phi}+\frac{\partial v_z}{\partial z} \text{ in cylindrical coodinates} \\ \vec\nabla\cdot\vec v &= \frac{1}{r^2}\frac{\partial \left(r^2 v_r\right)}{\partial r} + \frac{1}{r \sin(\theta)}\frac{\partial \left(\sin(\theta)\ v_\theta\right)}{\partial \theta}+\frac{1}{r \sin(\theta)}\frac{\partial v_\phi}{\partial \phi} \text{ in spherical coodinates}\end{align}\]
FIXME
The magnitude and direction of the gradient depends on the behavior of the function infinitesimally near the point of interest. One implication of this is that the gradient does not point in the direction of maxima a finite distance away (except sometimes accidentally), but rather in the direction of steepest slope at the point of interest.
The divergence at a point is a scalar. Taking the divergence of a function yields a scalar at every value in the domain of that function: a scalar field
For each partial derivative term in the divergence (in orthogonal coordinate systems), the direction of the component involved and the direction of the change agree (e.g. the $\textbf{x}$'s match in $\frac{\partial v_\textbf{x}}{\partial \textbf{x}}$.)
In any coordinate system, there exists a formula for the curl. Examples include:\[\vec\nabla\times\vec v = \left(\frac{\partial v_z}{\partial y}-\frac{\partial v_y}{\partial z}\right)\hat x + \left(\frac{\partial v_x}{\partial z}-\frac{\partial v_z}{\partial x}\right)\hat y + \left(\frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y}\right)\hat z \text{ in rectangular coodinates}\]\[\vec\nabla\times\vec v = \left(\frac{1}{s}\frac{\partial v_z}{\partial \phi} - \frac{\partial v_\phi}{\partial z}\right) \hat s + \left(\frac{\partial v_s}{\partial z} - \frac{\partial v_z}{\partial s}\right) \hat \phi + \frac{1}{s}\left(\frac{\partial \left(s\ v_\phi\right)}{\partial s} - \frac{\partial v_s}{\partial \phi}\right) \hat z \text{ in cylindrical coodinates}\]\[\vec\nabla\times\vec v = \frac{1}{r \sin(\theta)}\left(\frac{\partial \left(\sin(\theta)\ v_\phi\right)}{\partial \theta} - \frac{\partial v_\theta}{\partial \phi}\right) \hat r + \frac{1}{r}\left(\frac{1}{\sin(\theta)}\frac{\partial v_r}{\partial \phi} - \frac{\partial \left(r\ v_\phi\right)}{\partial r}\right)\hat \theta +\frac{1}{r} \left(\frac{\partial \left(r\ v_\theta\right)}{\partial r} - \frac{\partial v_r}{\partial \theta}\right) \hat \phi \text{ in spherical coodinates}\]
The divergence is geometric (i.e. it is independent of coordinate system)
ENTER LONG DESCRIPTION
For each partial derivative term in the curl (in orthogonal coordinate systems), the direction of the component involved and the direction of the change differ (e.g. $\textbf{$\alpha$} \neq \textbf{$\beta$}$ in $\frac{\partial v_\textbf{$\alpha$}}{\partial \textbf{$\beta$}}$.)
The curl is geometric (i.e. it is independent of coordinate system)
The curl is a particular geometric combination of partial derivatives
While the magnitude of the electric field is equal to the gradient of the electric potential, the electric field points in the opposite direction of the gradient of the electric potential, and thus $\vec E = - \vec \nabla V$.
FIXME
FIXME
[T = \left(\frac{\partial U}{\partial S}\right)_V] [p = -\left(\frac{\partial U}{\partial V}\right)_S]
FIXME
FIXME
The derivative with respect to $x$ of $x^A$ is $A \cdot x^{A-1}$.

At a cusp (or kink) in a curve, the derivative (and it's value) are not defined.
When taking the derivative of a product with $n$ factors, the product rule gives that this derivative is equal a sum of $n$ terms, the $i$th of which is the original function but with the $i$th factor replaced by the derivative of the $i$th factor: $\frac{d}{dt}(xy)=\frac{dx}{dt} y+x \frac{dy}{dt}$

For a smooth, two dimensional function, a tangent line exists at any point and in any direction.
- The total divergence in a volume is the same as the total flux out of its surface.[]2) The divergence theorem is used to move between the integral and differential forms of Gauss's law.[]3) Dimensions are the same
FIXME
FIXME
The gradient of an $n$ dimensional function is $n$ dimensional. This is not to be confused with the gradient having the same physical dimensions (e.g., Newtons) as the original function.
If the total flux through a closed surface is not zero, then the divergence of the function at that point is non-zero.
FIXME
FIXME
While it may be possible to conceptualize a particular derivative, such as $\left(\frac{\partial U}{\partial S}\right)_{V},$ Where $U$ is internal energy, $S$ is entropy, and $V$ is volume, that does not mean that the particular derivative can be directly measured. In the above example, the entropy $S$ is not measurable.