Stokes' Theorem relates line integrals of vector fields to surface integrals of vector fields.
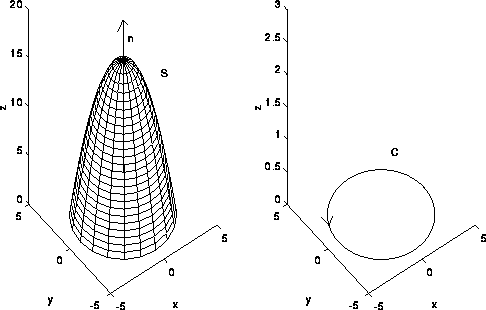
Consider the surface S described by the parabaloid z=16-x^2-y^2 for z>=0, as shown in the figure below.

Let n denote the unit normal vector to S with positive z component. The intersection of S with the z plane is the circle x^2+y^2=16. Let C denote this circle traversed in the counter clockwise direction. If F is a vector field with continuous partial derivatives in some region containing S, then Stokes' Theorem states
![]()
In general C is the boundary of S and is assumed to be piecewise smooth.
For the above equality to hold the direction of the normal vector n and the direction in which C is traversed must be consistent. Suppose that n points in some direction and consider a person walking on the curve C with their head pointing in the same direction as n. For consistency C must be traversed in such a way so that the surface is always on the left.
Example
Verify Stokes' Theorem for the surface S described above and the vector field F=<3y,4z,-6x>.
Let us first compute the line integral. The curve C can be parameterized by the vector function r(t)=<4cos(t),4sin(t),0> and r'(t)=<-4sin(t),4cos(t),0> for 0<=t<=2*pi. Recall that
![]()
In this case, F=<12sin(t),0,-24cos(t)>. The line integral is given by
![]()
Now, let us compute the surface integral. Recall that for F=<P,Q,R>,
![]()
For our vector field, the curl is <-4,6,-3>. For z=g(x,y)=16-x^2-y^2 the normal vector to S pointing in the positive z direction is given by <-g_x,-g_y,1>=<2x,2y,1>. Using the formula for the surface integral of a vector field, we have
![]()
where R is the disk 0<=x^2+y^2<=16, the projection of S onto the xy plane. The expression on the right is
![]()
a double integral.
It is convenient to convert to polar coordinates to compute the double integral. The region of integration is 0<=r<=4 and 0<=theta<=2*pi. Recall, that x=rcos(theta) and y=rsin(theta). The double integral becomes
![]()
The inner integral is
![]()
The final result for the inner integral is
![]()
The outer integral is
![]()
This result is same as that for the line integral!
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.