
This section contains material on
If you have taken a physics class, you have probably encountered the notion of work in mechanics.

If a constant force of F (in the direction of motion) is applied to move an object a distance d in a straight line, then the work exerted is
![]()
The unit for force is N (newton) and the unit for distance is m (meter). The unit for work is joule=(newton)(meter).
Now suppose that the there is an angle theta between direction in which the constant force is applied and the direction of motion.

In this case the work is given by:
![]()
Here |F| is the magnitude of the force and |d| is the distance. Let us treat force as a vector and let D be the vector from the starting point to the ending point. We can express the above formula in terms of vectors, we have
![]()
where the dot means the vector dot product. This formula is valid in 2 or three dimensions.
Line Integral of a Vector Field
The above formulas for work assume that the object moves in a straight line and that the force and the angle between the direction of the force and the direction of motion are constant.
Suppose that the object is moved along a curve C in the xy plane In addition, suppose that the force is given by the vector field F=<P(x,y),Q(x,y)>. What is the work required to move the object?
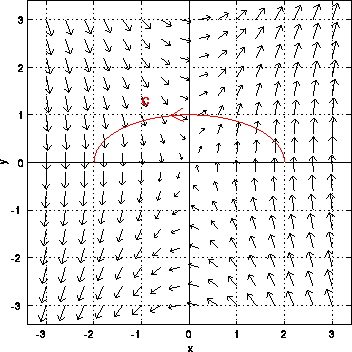
The figure above shows the curve C and the vector field. The object is moved in the direction indicated by the arrow on the curve. To compute the work, parameterize the curve C by the vector function r(t)=<x(t),y(t)> with a<=t<=b, where r(a) is the initial point and r(b) is the final point. Let us consider the work required to move the object on an infinitesimal piece of the curve from position r(t) to r(t+dt).

This piece of the curve is a straight line, since dt is infinitesimal. The force on the object and the angle between the force and the direction of motion is constant along the infinitesimal piece. We will assume that the force is the value at t, F(x(t),y(t)). It can be shown
![]()
Hence, the work to move the object on this part of the curve is
![]()
The total work to move the object along the entire curve is
![]()
The last integral above is the notation for the line integral of a vector field along a curve C.
Notice that
![]()
Hence, from previous work on line integrals, we have
![]()
Line integrals of vector fields extend to three dimensions. If F=<P(x,y,z),Q(x,y,z),R(x,y,z)>, then
![]()
In the figure above it is shown that C is traversed in the counter clockwise direction. What if we traverse C in the clockwise direction? Let -C denote the line integral on C in the clockwise direction. Then it can be shown that
![]()
How much work is required to move an object in the vector field F=<y,3x> along the upper part of the ellipse x^2/4+y^2=1 from (2,0) to (-2,0)?
A plot of the vector field and the curve is shown above. The curve can be parameterized as r(t)=<2cos(t),sin(t)> with 0<=t<=pi. Hence, r'(t)=<-2sin(t),cos(t)>. The total work is
![]()
If one traverses the curve starting at (-2,0) and ending at (2,0), then the value of the line integral is -2*pi.
Dependence of Work on the Path
In general, the amount of work required to move the object from (2,0) to (-2,0) depends on the path taken! Suppose that we move the object in the above vector field on the real axis instead of on the ellipse. In this case, r(t)=<2-t,0>, where t goes from 0 to 4. In this case r'(t)=<-1,0>. The line integral is
![]()
No work is required! This can be seen in the plot above. The vector field F is orthogonal to the horizontal direction if y=0. (Note we have F=<0,3x> for y=0.) Hence, if one moves an object along the x-axis, no work is expended.
If the vector field is conservative, then the line integral from point A to point B is independent of path.
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.