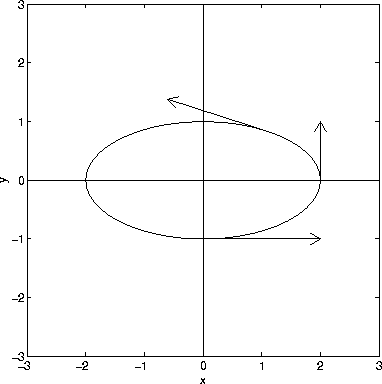
This page has information about
The Derivative of a Vector Function
The derivative of a vector function r=<f(t),g(t),h(t)> is r'(t)=<f'(t),g'(t),h'(t)>. Note one differentiates each component independently. For example, consider the 2-dimensional space curve defined by r(t)=<2cos(t),sin(t)>. The derivative is r'(t)=<-2sin(t),cos(t)>. If r(t) is the position function of a particle, then r'(t) is the velocity function, analogous to the velocity function in one dimension.
Here are various rules for differentiation of vector functions:
There is a nice geometric description of the derivative r'(t). The derivative r'(t) is tangent to the space curve r(t). This is shown in the figure below, where the derivative vector r'(t)=<-2sin(t),cos(t)> is plotted at several points along the curve r(t)=<2cos(t),sin(t)> with 0<=t<=2*pi.
The unit tangent vector, denoted T(t), is the derivative vector divided by its length:
![]()
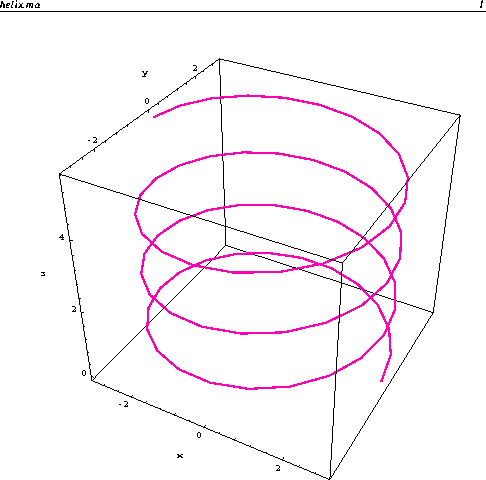
Suppose that the helix r(t)=<3cos(t),3sin(t),0.25t>, shown below, is a piece of string. If we straighten out the string and measure its length we get its arc length.
To compute the arc length, let us assume that the vector function r(t)=<f(t),g(t),h(t)> represents the position function of a particle. In an infinitesimal time interval from t to t+dt the particle essentially travels in a straight line. The distance traveled is
![]()
From the discussion above, the velocity of the particle is r'(t). Hence,
![]()
The distance traveled is
![]()
If the initial time is t=a and the final time is t=b, then the total distance traveled is
![]()
For the helix above r'(t)=<-3sin(t),3cos(t),0.25> and 0<=t<=7*pi. Hence,
![]()
Let r(t) for a<=t<=b be a space curve. The arc length function s(t) measures the length of the curve from a to t. Based on our discussion above,
![]()
For the helix above, where a=0, the arc length function is given by
![]()
Note that
![]()
Parameterization with Respect to Arc Length
There is not a unique way to define a space curve. For example, the vector functions
![]()
and
![]()
both trace out the helix in the figure above. Think of r(t) as representing the position of a particle. The difference between the two descriptions (or parameterizations) of the helix is the speed at which the particle travels. The particle travels twice as fast in the second parameterization than in the first parameterization.
A natural parameterization for a space curve is with respect to arc length. The distance along a space curve is independent of parameterization. This simply means that the total distance traveled along a curve is independent of the speed.
To parameterize a space curve r(t) we compute the we invert the arc length function s(t) to get t(s). The new parameterization for the curve is r(t(s)). For the helix r(t)=<3cos(t),3sin(t),0.25t> (0<=t<=7*pi), we have s(t)=sqrt(9.0625)t. Hence t=s/sqrt(9.0625). Let c=sqrt(9.0625). We have
![]()
Here is the significance of parameterization with respect to arc length: s=0 corresponds to the initial point on the helix; r(s=1) corresponds to the point one unit of length along the curve from the initial point; and, in general r(s=s_1) is the point s_1 units of length along the curve from the initial point.
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.