The following result for line integrals is analogous to the Fundamental Theorem of Calculus.
Let C be a curve in the xyz space parameterized by the vector function r(t)=<x(t),y(t),z(t)> for a<=t<=b. Suppose that f(x,y,z) is a differentiable function whose gradient grad f=<f_x,f_y,f_z> is continuous on C. Then
![]()
The above result states that the line integral of a vector field derived from a gradient depends only on the function f(x,y,z) and on the initial point (x(a),y(a),z(a)) and final point (x(b),y(b),z(b)) and not on the particular curve C. Hence, the integral is path independent. (Compare this with an example of a path dependent line integral.)
We have given the result for a function f(x,y,z) of three variables and a curve in 3 dimensional space. The above result is valid for functions of any number of variables.
Example
Verify the Fundamental Theorem for line integrals for the case that C is the top half of the circle x^2+y^2=1 traversed in the counter clockwise direction and
![]() .
.
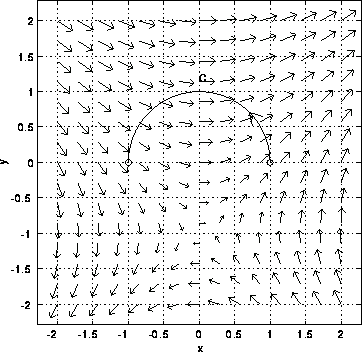
A plot of the vector field and C is given above. The initial point is (1,0) and the final point (-1,0). It follows that the the value of the integral is
![]()
This is an example where f is a function of two variables so we are dealing with a vector field in the xy plane. The vector field is
![]()
We can parameterize the curve C by vector function r(t)=<cos(t),sin(t)> for 0<=t<=pi. On this curve the vector field is <sin(t)+1,cos(t)> and r'(t)=<-sin(t),cos(t)>. It follows that
![]()
Cleaning this up, we have
![]()
Here we have used the identity cos^2(t)-sin^2(t)=cos(2t).
In this example the gradient function <y+1,x> is continuous at all points in the xy plane. The line integral of <y+1,x> from (1,0) to (-1,0) is equal to -2 for any curve joining these two points.
Conservative Vector Fields
Recall that a vector field F is conservative if there is a function f such that F=grad f. If we know that a vector field is conservative, then we can apply the Fundamental Theorem. The following result gives a test for determining if a vector field is conservative.
If F is a vector field defined in all of xyz space whose component functions have continuous partial derivatives and curl F=0, then F is a conservative vector field.
The above criterion doesn't say how to find the function f. It just says that a function f exists.
Example
Here is an example: determine if F=<z,2yz,x+y^2> is conservative.
Notice that each component of F has continuous partial derivatives with respect to x, y, and z. If F=<P,Q,R>, then the definition of curl is
![]()
A quick calculation shows that indeed curl F=0.
The above shows that there exists a function f(x,y,z) such that grad f=F=<P,Q,R>. How do we find the function f?
We know that
![]()
![]()
![]()
We integrate to determine f. By the Fundamental Theorem of Calculus
![]()
In the above integral y and z are treated as constants. We must add a function of G(y,z) because G_x(y,z)=0. Doing this calculation, we find
![]()
To determine G(y,z) we use the information that f_y=2yz and f_z=x+y^2. We have
![]()
This last equation implies
![]()
To determine G(y,z) we integrate with respect to y and add a constant function of z:
![]()
This means
![]()
To find H(z) we differentiate with respect to z:
![]()
This last equation implies H'(z)=0. Hence, H(z)=constant. The final result is
![]()
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.