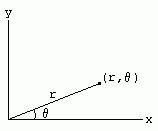
Introduction
The usual Cartesian coordinate system can be quite difficult to use in certain situations. Some of the most common situations when Cartesian coordinates are difficult to employ involve those in which circular, cylindrical, or spherical symmetry is present. For these situations it is often more convenient to use a different coordinate system.
In polar coordinates, a point in the plane is determined by its distance r from the origin and the angle theta (in radians) between the line from the origin to the point and the x-axis (see the figure below).
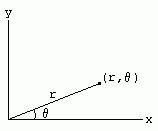
It is common to represent the point by an ordered pair (r,theta). Using standard trigonometry we can find conversions from Cartesian to polar coordinates
![]()
and from polar to Cartesian coordinates
![]()
Example
The point with rectangular coordinates (-1,0) has polar coordinates (1,pi) whereas the point with rectangular coordinates (3,-4) has polar coordinates (5,-0.927).
Note that a point does not have a unique polar representation. The points
![]()
are equivalent for any integer n.
The curves r=constant and theta=constant are a circle and a half-ray, respectively.
Cylindrical coordinates are obtained by replacing the x and y coordinates with the polar coordinates r and theta (and leaving the z coordinate unchanged).
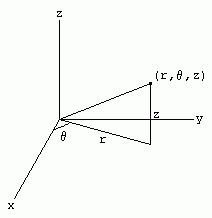
Thus, we have the following relations between Cartesian and cylindrical coordinates:
From cylindrical to Cartesian:
![]()
From Cartesian to cylindrical:
![]()
As an example, the point (3,4,-1) in Cartesian coordinates would have polar coordinates of (5,0.927,-1).Similar conversions can be done for functions. Using the first row of conversions, the function
![]()
in Cartesian coordinates would have a cylindrical coordinate representation of
![]()
Cylindrical coordinates are most convenient when some type of cylindrical symmetry is present. The surfaces r=constant, theta=constant, and z=constant are a cylinder, a vertical plane, and a horizontal plane, respectively.
The coordinates used in spherical coordinates are rho, theta, and phi. Rho is the distance from the origin to the point. Theta is the same as the angle used in polar coordinates. Phi is the angle between the z-axis and the line connecting the origin and the point.
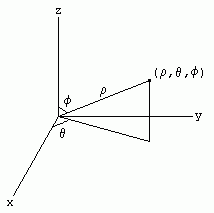
The following are the relations between Cartesian and spherical coordinates:
From spherical to Cartesian:
![]()
From Cartesian to spherical:
![]()
Relations between cylindrical and spherical coordinates also exist:
From spherical to cylindrical:
![]()
From cylindrical to spherical:
![]()
The point (5,0,0) in Cartesian coordinates has spherical coordinates of (5,0,1.57). The surfaces pho=constant, theta=constant, and phi=constant are a sphere, a vertical plane, and a cone (or horizontal plane), respectively. Spherical coordinates are of course very useful when any type of spherical symmetry is present.
Example: Many physical situations have spherical symmetry. The gravitational field of a single body and the electric field of a point charge exhibit spherical symmetry. Formulas used in these situations almost always involve r, theta, and phi and not x, y, and z.
It should be noted that formulas for objects like the gradient, curl, and divergence have a different form in different coordinate systems. Always be careful to use the proper formula when dealing with these objects.
[Vector Calculus Home] [Math 254 Home] [Math 255 Home] [Notation] [References]
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.