Derivation of formula for Flux
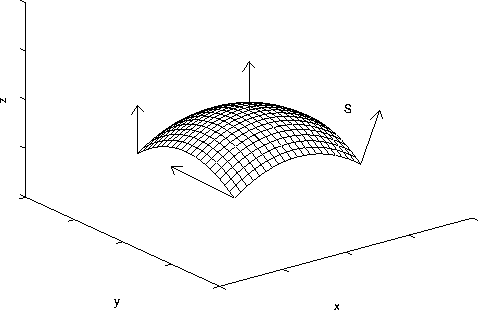
Suppose the velocity of a fluid in xyz space is described by the vector field F(x,y,z). Let S be a surface in xyz space. The flux across S is the volume of fluid crossing S per unit time. The figure below shows a surface S and the vector field F at various points on the surface.

What is the formula for the flux? Let us consider the flux through an infinitesimal piece of the surface with area dS above the point (x_0,y_0) in the xy plane. (The surface is denoted by the dotted region.) Let n denote the unit normal vector to the surface. Let us suppose that the velocity vector F(x_0,y_0,z_0) of the fluid makes an angle theta with the unit normal. In one unit of time a blob of fluid of length |F|=|F(x_0,y_0,z_0)| will pass through the surface. (The blob is in the shape of a parallelepiped.)
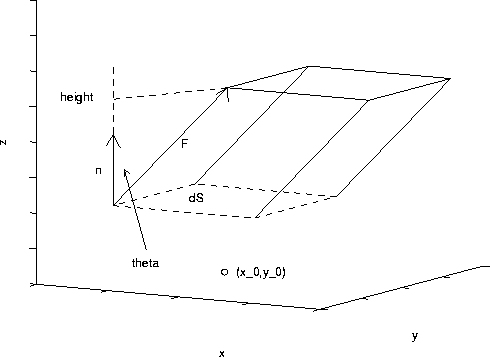
The volume of this fluid is
![]()
The base area is dS. The height is equal to |F|cos(theta). Hence, we have
![]()
Here we have used the fact that |n|=1 and the property of the dot product. The total flux through the surface is
![]()
This is a surface integral.
We can write the above integral as an iterated double integral. Suppose that the surface S is described by the function z=g(x,y), where (x,y) lies in a region R of the xy plane. The unit normal vector on the surface above (x_0,y_0) (pointing in the positive z direction) is
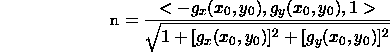
The surface area of an infinitesimal piece of the surface above a infinitesimal region in the xy plane with area dA containing (x_0,y_0) is given by
![]()
Hence, it follows that the total flux is
![]()
If we are asked for the flux in the negative z direction, then we use the vector <g_x(x,y),g_y(x,y),-1> for the normal direction.
Formula for Flux for Parametric Surfaces
Suppose that the surface S is described in parametric form:
![]()
where (u,v) lies in some region R of the uv plane. It can be shown that
![]()
Here, x means the cross product. Note, one may have to multiply the normal vector r_u x r_v by -1 to get the correct direction.
Example
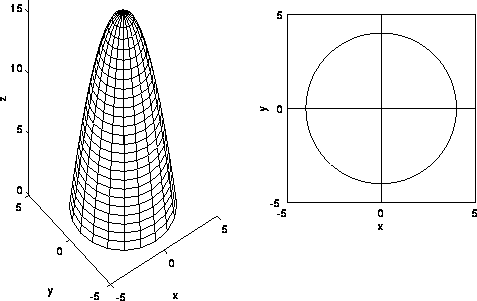
Find the flux of the vector field <y,x,z> in the negative z direction through the part of the surface z=g(x,y)=16-x^2-y^2 that lies above the xy plane (see the figure below).
For this problem:
![]()
It follows that the normal vector is <-2x,-2y,-1>. Computing Fo<-2x,-2y,-1>, we have
![]()
Here we use the fact that z=16-x^2-y^2. Hence, the integral becomes
![]()
The region R is the disk of radius 4 centered at the origin shown below. It is convenient to convert to polar coordinates. The region of integration is 0<=r<=4 and 0<=theta<=2*pi. Substituting,
![]()
we have
![]()
Here we have used the fact that x^2+y^2=r^2. (We can also integrate with respect to theta first, then r.) The inner integral with respect to r yields (remember theta is held constant)
![]()
which is equal to
![]()
The inner integral is
![]()
Hence, the flux through the surface in the downward z direction is -128*pi cubic units per unit time. This means a negative amount of fluid crosses the surface in the downward direction. In other words, there is a flux of 128*pi cubic units per unit time in the upward z direction.
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.