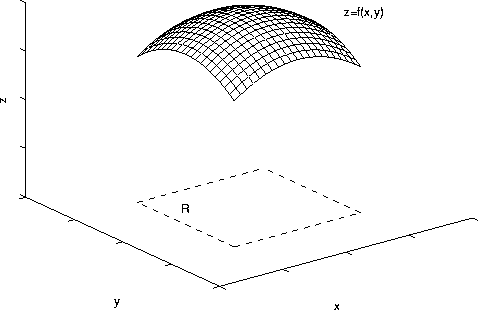
Let f(x,y) be a differentiable function. As we have seen, z=f(x,y) defines a surface in xyz-space. In some applications, it necessary to know the surface area of the surface above some region R in the xy-plane. See the figure.

The formula for the surface area is
![]()
This is a double integral.
Example
What is the surface area of the plane z=2x+3y above the rectangle with -1<=x<=2 and 0<=y<=2? In this case f_x=2 and f_y=3. Applying the above formula, the surface area S is given by
![]()
Since, the region of integration R is a rectangle and the integrand is continuous, the value of the integral is independent of the order of integration. It can be shown that S=6*sqrt(14).
Example
Find the surface area of the part of the paraboloid z=16-x^2-y^2 that lies above the xy plane (see the figure below).
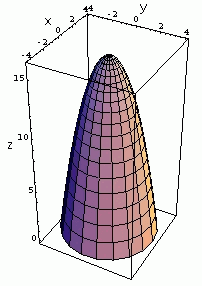
The region R in the xy-plane is the disk 0<=x^2+y^2<=16 (disk or radius 4 centered at the origin).
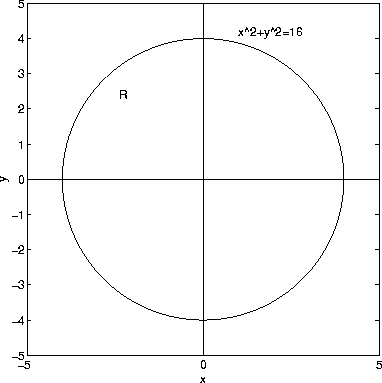
For this problem, f_x=-2x and f_y=-2y. Hence, the surface area S is given by
![]()
Since R is a disk, it convenient to convert the above integral into polar coordinates. The disk R satisfies 0<=r<=4 and 0<=theta<=2*pi. In addition,
![]()
The surface area is given by the integral
![]()
Both iterated integrals above can be computed in a straightforward manner. The final answer is
![]()
Derivation of the Surface Area Formula
It is instructive to derive the surface area formula. We start by assuming that the surface is the plane:
![]()
Consider a part of the plane above a rectangle in the xy-plane with x_0<=x<=x_0+dx and y_0<=y<=y_0+dy, as shown in the figure below.
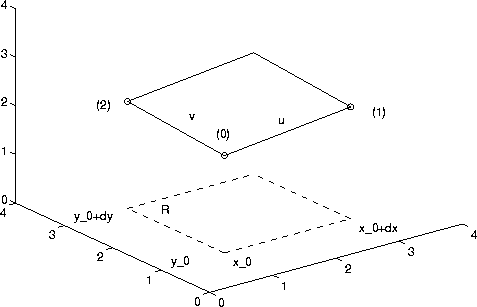
Let u be the vector from point 0 to point 1 and v be the vector from point 0 to point 2. The area of the plane above the rectangle R is
![]()
Given the formula for the plane, point 0 is (x_0,y_0,z_0), point 1 is (x_0+dx,y_0,z_0+adx), point 2 is (x_0,y_0+dy,z_0+bdy). Hence,
![]()
Taking the cross product, we have
![]()
The area is
![]()
Note dxdy is the area of the rectangle in the xy plane.
For a general surface z=f(x,y), we can approximate the area of the surface over the small rectangle in the figure above by the tangent plane through (x_0,y_0,z_0). The equation of the tangent plane is
![]()
This last equation is the same as the equation for the plane with a replaced by the x derivative and b replaced by the y derivative. Hence, the area is
![]()
In the case that the region R is not a rectangle we replace dxdy by dA, the area of a general infinitesimal region containing (x_0,y_0).
[Vector Calculus Home] [Math 254 Home] [Math 255 Home] [Notation] [References]
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.