Functions of Several Variables

Introduction

You are likely familiar with functions in one variable and their graphs. Given a value of x, y(x) returns the value of the function. Here x is the independent variable and y is the dependent variable. Here are some examples of functions of one variable that you have likely seen before:

• position function of a particle y(t), where t is time and y(t) is the position
• velocity and acceleration functions v(t) and a(t), where t is time
• density function of a one-dimensional bar p(x): x is the position along
  the bar and p(x) is the density in kg/m.

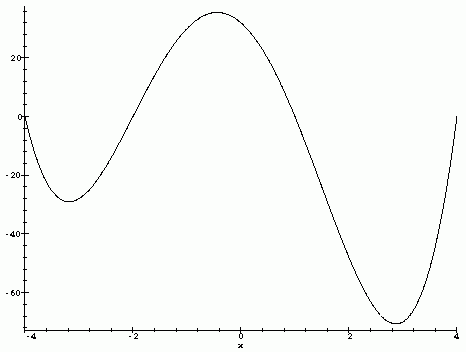
A function of one variable can be represented by a simple graph. The horizontal axis corresponds to the independent variable and the vertical axis corresponds to the dependent variable. The value of the function corresponds to the height above the horizontal axis. The graph below is of the function f(x)=x^4+x^3-18x^2-16x+32.

Functions of Several Variables

A function of several variables has several independent variables. An example is temperature on the earth's surface. Suppose that we wish to describe the temperature at a particular instant in time. Temperature depends on position. It takes two coordinates to represent position on the earth's surface, longitude and latitude. Let the variables x and y represent these quantities, respectively. Then we can define T(x,y) to be the temperature function. Given x and y we can determine the temperature. This is a function of 2 variables.

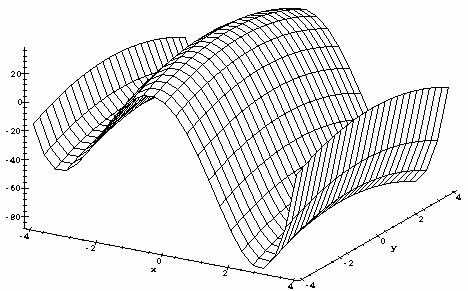
A function of 2 variables is represented graphically by a surface in three-dimensional space. For the temperature function above, a position on the earth's surface is represented by a point in the xy-plane. The temperature at that position is represented by the height of surface above the xy-plane. The figure below plots the surface corresponding to the function f(x,y)=x^4+x^3-18x^2-16x+32-y^2.

There are many examples of functions of several variables:

• Temperature functions T(x,y,t), where x and y represent the
  position and t represents time
• Density functions p(x,y,z) for a three dimensional solid, where
  x, y, and z represent the position coordinates and p(x,y,z) is
  the density in kg/m^3
• Concentration functions C(x,y,z,,t), where x,y, and z represent
  position, t is time, and C(x,y,z,t) is the concentration of a
  substance in a solution.

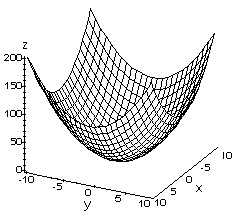
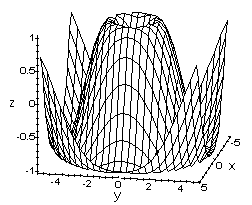
Below are graphs of some examples of functions of two variables. On the left is a graph of the function z=x^2+y^2 and on the right is a graph of the function z=sin(sqrt(x^2+y^2)).

It is difficult to completely represent a function of more than 2 variables graphically, since for a function of n variables, n+1 dimensional space is required.

[Vector Calculus Home] [Math 254 Home] [Math 255 Home] [Notation] [References]

Copyright © 1996 Department of Mathematics, Oregon State University

If you have questions or comments, don't hestitate to contact us.