For some regions R, it convenient to convert to polar coordinates in order to evaluate the double integral
![]()
Consider the sector a<=r<=b, c<=theta<=d shown in the figure below.
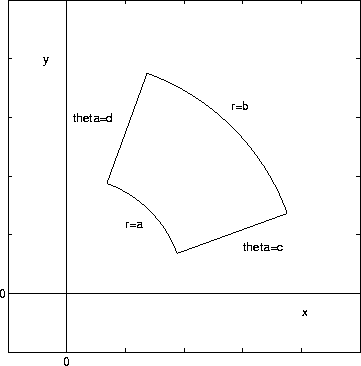
Recall that x=r*cos(theta) and y=r*sin(theta). The double integral is given by:
![]()
In the above formula one integrates with respect to theta first, then r. Alternatively, one could integrate with respect to r first, then theta.
Discussion of the Iterated Integral in Polar Coordinates
In the case of double integral in polar coordinates we made the connection dA=dxdy. dxdy is the area of an infinitesimal rectangle between x and x+dx and y and y+dy. In polar coordinates, dA=rd(theta)dr is the area of an infinitesimal sector between r and r+dr and theta and theta+d(theta). See the figure below.
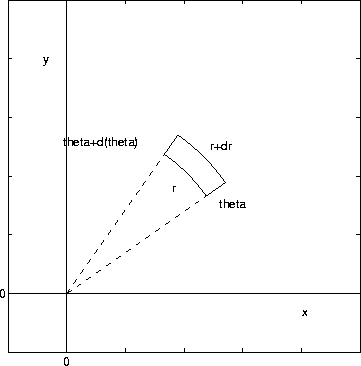
The area of the region is the product of the length of the region in theta direction and the width in the r direction. The width is dr. The length is d(theta)*r, the arclength of a part of a circle of angle d(theta). (The radius is essentially constant in the region since dr is infinitesimal.)
Example
Consider the integral with f(x,y)=2x+3y^2 where R is the region between the circles x^2+y^2=1 and x^2+y^2=4. In this case 1<=r<=2 and 0<=theta<=2*pi. We can convert the function f(x,y) into polar coordinates with the substitutions x=r*cos(theta) and y=r*sin(theta). The iterated integral is
![]()
We integrate with respect to theta first, then r. Alternatively, we have
![]()
Examples of how to evaluate iterated integrals are given in the double integrals page.
General Regions
If the region R is of the form g_1(r)<=theta<=g_2(r) with a<=r<=b, as shown in the figure below,
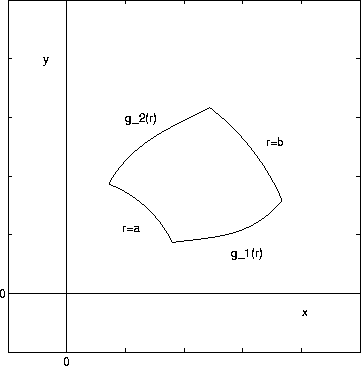
then the double integral is given by the iterated integral
![]()
If the region R is of the form h_1(theta)<=r<=h_2(theta) with c<=theta<=d, as shown in the figure below,
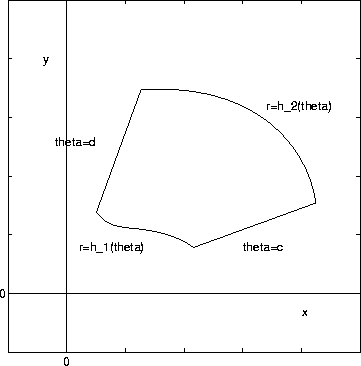
then the double integral is given by the iterated integral
![]()
[Vector Calculus Home] [Math 254 Home] [Math 255 Home] [Notation] [References]
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.