Malgorzata Peszynska

Research

My research interests are in mathematical and computational modeling of real-life phenomena such as flow, transport, and other coupled processes. I am interested in i) modeling and the analysis of models, ii) construction and analysis of appropriate computational techniques, and iii) simulations that contribute to our understanding and management of these phenomena. My work in (i-ii) primarily involves finite element methods, and that in iii) their multiscale aspects and high performance computing implementations.

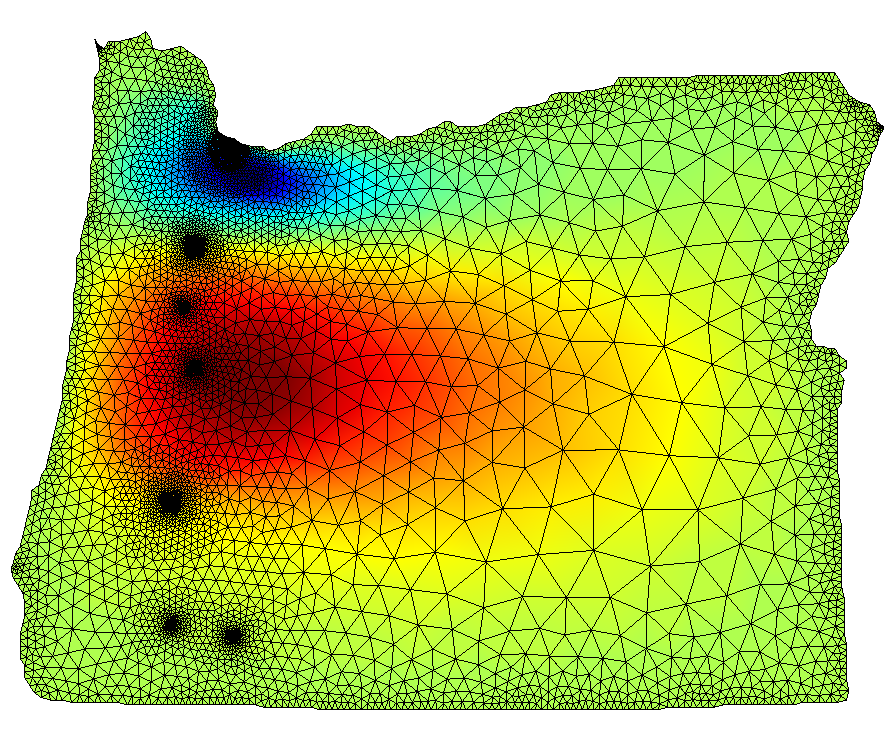
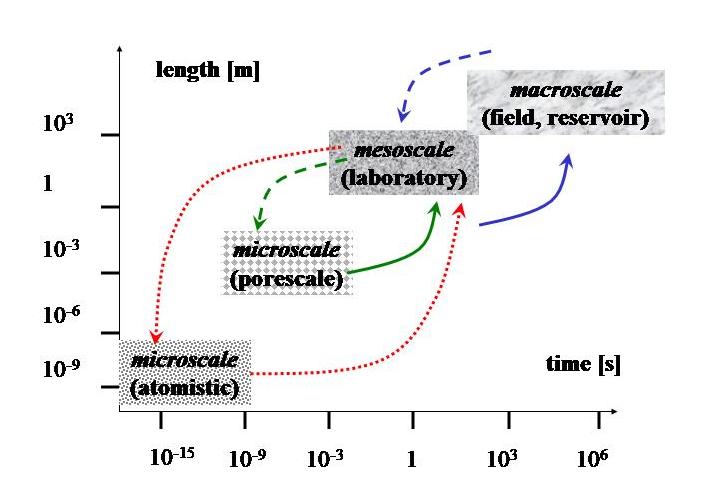
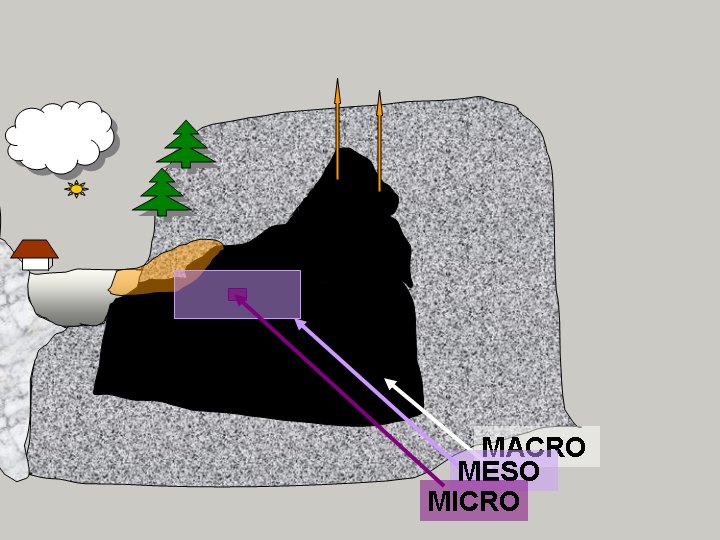
Studying how fluids flow, react, change phase, and interact with the surrounding environment, is fundamental for understanding natural phenomena and for designing how humans can control and engineer various processes. The applications I have worked with range from the flow and transport in groundwater and hydrocarbon reservoirs (kilometer scale) through the flow of nutrients and the growth of microbial species at porescale (micron scale), down to the angstrom scale of semiconductors. The associated time scales range from years or kiloyears to hors to nanoseconds. Multiscale modeling of coupled processes is central to my research, and we use different analysis and simulations techniques in each case.

Computing

Contemporary modeling of coupled multiscale processes requires computation, because the true solutions to complex models are almost never available in a closed form. We use analysis of models to establish their qualitative properties which we must prove hold for numerical solutions. Rigorous numerical analysis determines if the algorithms are correctly approximating the true solutions.

Implementation of efficient algorithms that scale to very large problems and can run on petascale platforms is an art in itself. You can probably solve a 3x3 linear system by hand, implement a cellular-automata model with 100 cells in your phone's spreadsheet, and solve 1d or 2d Poisson's problem with O(10K-100K) unknowns on a laptop or workstation. However, high-performance computing techniques and parallel implementation are essential to deal with O(10M) unknowns such as for accurate fluid modeling in 3D.

Students new to computing can find some information at the "for students" page. Also, see the pages with some code and software that we developed. (It is permanently being updated).
See also the listing of other software on github and CODE CAPSULES.

Hybrid models: across scales and processes

Coupling of models across the scales (left) and coupled phenomena at multiple scales in the environment.

One of our objectives is to develop hybrid models coupling the different scales, at best dynamically. The models we use are typically nonlinear coupled differential equations at multiple scales and have different dynamics at each scale. At some scales we use discrete deterministic and non-deterministic models such as network, cellular automata, and other statistical mechanics-based models. Some data is available (such as porescale images), and we try to learn about the processes and the models from this data. When a traditional model is too complex, we try to replace it by reduced models. We are also considering the ways to parametrize and evaluate the uncertainty of solutions. Finally, since some of the simulations are extremely complex, we explore ways to understand and recreate the dynamics of certain processes from data, via statistical mechanics and/or machine learning.