Robert L. Higdon

Professor of Mathematics
Oregon State University

Office: Kidder 294B
Phone: (541) 737-5150
Fax: (541) 737-0517
E-mail: robert.higdon@oregonstate.edu or higdon@math.oregonstate.edu

Postal address:

Department of Mathematics
Oregon State University
Kidder Hall 368
Corvallis, Oregon 97331-4605

Education:

University of Missouri - Columbia, B.A., Dec. 1975
Stanford University, Ph.D., Aug. 1981

Teaching

Fall quarter 2024

Math 311, Advanced Calculus, 9:00-9:50 MWF.

Matlab notes

Notes on Computational Mathematics: Matlab, by R. L. Higdon. (PDF, 225 K.) These notes describe the basics of Matlab, plus some mathematical topics. The notes are rather old, but the contents are still valid.

Research

Research interests

Applied mathematics, numerical solution of partial differential equations.
Some of my past work was devoted to absorbing boundary conditions and initial-boundary value problems. More recently, I have been working on problems related to the numerical modeling of ocean circulation, including time-stepping and multiple time scales. Currrently I am looking at some matters related to the possible usage of discontinuous Galerkin methods for spatial discretization in multi-layer ocean models.

Example

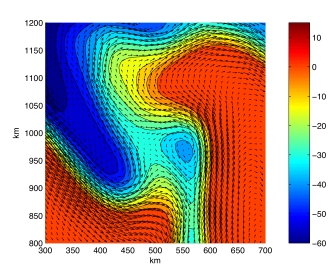
The figure to the right was produced from a numerical computation that tested a timestepping method and other algorithms for solving a system of partial differential equations that describes large-scale ocean circulation. It is similar to a black-and-white figure in the 2005 JCP paper listed below. The curves and varying colors represent a contour plot of the height of the free surface at the top of the fluid, and the arrows represent the horizontal fluid velocity. In the color bar, the units are centimeters. Due to the effects of the earth's rotation, the horizontal velocity is approximately perpendicular to the horizontal pressure gradient, which means that the fluid flows along curves of constant elevation.

A larger version of this plot can be obtained here. This test computation was performed on a square spatial domain; a black-and-white contour plot for the entire fluid domain is given in the next figure.

Some publications

R. L. Higdon, A two-level time-stepping method for layered ocean circulation models: further development and testing (PDF), Journal of Computational Physics, vol. 206, pp. 463-504, 2005.

R. L. Higdon, Numerical modelling of ocean circulation (PDF), Acta Numerica 2006, pp. 385-470. Acta Numerica is an annual volume, published by Cambridge University Press, that contains invited surveys on topics in numerical analysis and scientific computing.

R. L. Higdon, A comparison of two formulations of barotropic-baroclinic splitting for layered models of ocean circulation (PDF), Ocean Modelling, vol. 24, pp. 29-45, 2008.

R. L. Higdon, Physical and computational issues in the numerical modeling of ocean circulation (PDF). In Computational Challenges in the Geosciences, C. Dawson and M. Gerritsen, editors, The IMA Volumes in Mathematics and its Applications, volume 156, Springer, 2013. This volume is based on a workshop held in April 2011 at the Institute for Mathematics and its Applications, University of Minnesota.

R. L. Higdon, Pressure forcing and dispersion analysis for discontinuous Galerkin approximations to oceanic fluid flows (PDF), Journal of Computational Physics, vol. 249, pp. 36-66, 2013.

T. Ringler, M. Petersen, R. L. Higdon, D. Jacobsen, P.W. Jones, M. Maltrud, A multi-resolution approach to global ocean modeling, Ocean Modelling, vol. 69, pp. 211-232, 2013.

R. L. Higdon, Multiple time scales and pressure forcing in discontinuous Galerkin approximations to layered ocean models (PDF), Journal of Computational Physics, vol. 295, pp. 230-260, 2015.

R. L. Higdon, Discontinuous Galerkin methods for multi-layer ocean modeling: viscosity and thin layers (PDF), Journal of Computational Physics, vol. 401, publication 109018, 2020. 23 published pages.

R. L. Higdon, An automatically well-balanced formulation of pressure forcing for discontinuous Galerkin methods for the shallow water equations (PDF), Journal of Computational Physics, vol. 458, publication 111102, 2022. 25 published pages.

J. R. Lilly, G. Capodaglio, M. R. Petersen, S. R. Brus, D. Engwirda, R. L. Higdon, Storm surge modeling as an application of local time stepping in MPAS-Ocean, Journal of Advances in Modeling Earth Systems, 10.1029/2022MS003327, 16 published pages, 2023.

J. R. Lilly, D. Engwirda, G. Capodaglio, R. L. Higdon, M. R. Petersen, CFL optimized forward-backward Runge-Kutta schemes for the shallow-water equations, Monthly Weather Review, vol. 151, pp. 3191-3208, 2023.

Note: Except for the Acta Numerica paper, each of the linked PDF files is a personal typeset version instead of the final version as produced by the publisher, but the contents are the same. The personal typeset versions are posted here, for copyright reasons.

This page was last updated: June 13, 2024.