Figure 1: A torus in $\RR^3$.

Figure 2: Parameterizing the torus as a surface of revolution about the $z$-axis.

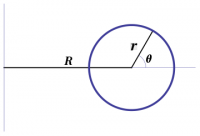
The torus $\TTT$, shown in Figure 1, can be parameterized as a surface of revolution about the $z$-axis, as shown in Figure 2, resulting in \begin{align} x &= (R+r\,\cos\theta)\,\cos\phi \\ y &= (R+r\,\cos\theta)\,\sin\phi \\ z &= r\,\sin\theta \end{align} from which it follows by direct computation that \begin{equation} ds^2 = r^2\,d\theta^2 + (R+r\,\cos\theta)^2\,d\phi^2 \label{dstorus} \end{equation} Alternatively, (\ref{dstorus}) follows directly from the Pythagorean theorem, using arclength to compute small distances in the $\theta$ and $\phi$ directions.

Our orthonormal basis of 1-forms is therefore \begin{align} \sigma^\theta &= r\,d\theta \\ \sigma^\phi &= (R+r\,\cos\theta)\,d\phi \end{align} The structure equations are now \begin{align} -\omega^\theta{}_\phi\wedge\sigma^\phi &= d\sigma^\theta = 0 \\ -\omega^\phi{}_\theta\wedge\sigma^\theta &= d\sigma^\phi = -r\,\sin\theta\,d\theta\wedge d\phi \end{align} from which it follows that \begin{equation} \omega^\theta{}_\phi = \sin\theta\,d\phi \end{equation} and therefore that \begin{equation} d\omega^\theta{}_\phi = \cos\theta\,d\theta\wedge d\phi = \frac{\cos\theta}{r(R+r\,\cos\theta)}\>\omega \end{equation} since $\omega^\phi{}_\theta=-\omega^\theta{}_\phi$, and where $\omega=\sigma^\theta\wedge\sigma^\phi$ is a choice of orientation. Thus, the Gaussian curvature of the torus is given by \begin{equation} K = \frac{\cos\theta}{r(R+r\,\cos\theta)} \end{equation}

This result makes sense: the curvature in the $\theta$ direction is clearly just $1/r$, and the curvature in the $\phi$ direction should go like the inverse radius, or $1/(R+r\,\cos\theta)$. But why is there a factor of $\cos\theta$?

Recall that the principal curvatures tell you how the normal vector is changing. Read this sentence carefully: the principal curvatures tell you how the normal vector to the surface is changing along (principal) directions in the surface. When computing the curvature of a circle, the relevant normal vector is the outward-pointing radial vector, which lies in the plane of the circle. However, when computing the curvature of a surface along a circle, the relevant normal vector is that of the surface. For circles on the torus in the $\theta$ direction, there is no difference; these two normal vectors are the same. However, for circles in the $\phi$ direction, this is not the case.

Consider the circles on the top or bottom of the torus. The surface normal vector is always straight up (or down); it does not change in the $\phi$ direction. Thus, one principal curvature vanishes at the top and bottom of the torus, and hence so does the Gaussian curvature.

Furthermore, on the outer half of the torus, the change in the normal vector in the $\phi$ direction has a positive component in that direction, whereas on the inner half of the torus, the opposite is true. This property is most easily visualized in the equatorial plane; since the surface normal vectors have opposite orientations on the inner and outer rings, the principal curvature in the $\phi$ direction has opposite signs there. The factor of $\cos\theta$ accounts precisely for the difference in angle between the normal vector to the surface, and the (horizontal) normal vector to the circles of constant “latitude”. 1)

Thus, the principal curvature in the $\phi$ direction, and hence the Gaussian curvature, must be positive on the outer half, and negative on the inner half (and zero in between).

This should not be surprising. The Gauss-Bonnet Theorem tells us that \begin{equation} \int_T K\,\omega = 2\pi \chi(\TTT) \end{equation} and it is easy to check by example that the Euler characteristic of a torus is zero, that is, $\chi(\TTT)=0$. Thus, the total curvature of any torus must be zero, so that regions of positive curvature must be counterbalenced by regions of negative curvature. This is a topological statement; no matter how you twist a torus, its total curvature must be zero.

Can a torus be flat, that is, can its curvature be zero everywhere? Surprisingly, the answer is yes — and if you have ever played a video game, it is likely that you have already encountered a flat torus. Take a rectangular piece of paper, and identify opposite edges; this is just the “wraparound” feature of many video games, in which leaving the screen on the right causes you to reenter the screen on the left, etc. The curvature is clearly zero; locally, it's just a piece of paper. And the topology is indeed that of a torus, as can be shown by experimentally determining the Euler characteristic.

Can you actually make such a torus? Not in three dimensions! This torus naturally lives in four dimensions, as can be seen by the following parameterization in $\RR^4$ \begin{align} x = r\,\cos\theta \\ y = r\,\sin\theta \\ z = s\,\cos\phi \\ w = s\,\sin\phi \end{align} which also shows why we often write the torus $\TTT$ as $\SSS^1\times\SSS^1$, the product of two circles.