- §1. Curves
- §2. Surfaces
- §3. Examples in 3D
- §4. Curvature
- §5. Curvature in 3D
- §6. Components
- §7. Bianchi Identities
- §8. Geodesic Curvature
- §9. Geodesic Triangles
- §10. Gauss-Bonnet Thm
- §11. The Torus
Curves
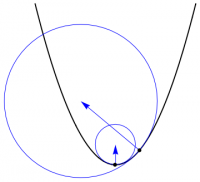
How much does a curve bend? Take the circle which best fits the curve at a given point, and use the radius of this circle to specify the curvature of the curve at that point. Since large circles have less curvature than small circles, define the curvature to be \begin{equation} \kappa = \frac{1}{r} \end{equation} where $r$ is the radius of the best-fit circle. The unit tangent vector to a curve is given by \begin{equation} \TT = \frac{d\rr}{|d\rr|} = \frac{d\rr}{ds} \end{equation} where, as usual, $s$ denotes arclength along the curve. For a circle, it is easy to see that \begin{equation} \frac{d\TT}{ds} = \frac{1}{r} \,\NN \end{equation} where $\NN$ is the inward-pointing normal vector. Since this computation depends only on the first derivative of the tangent vector, the result must be the same for the best-fit circle and for the curve itself. We have therefore shown that \begin{equation} \frac{d\TT}{ds} = \kappa \NN \label{dTds} \end{equation} where $\NN$ is the principal unit normal vector, which points in the direction of bending.
This construction is depicted in Figure 1, which shows the best-fit circle at two points on a parabola, together with vectors pointing to the center of each circle. The magnitude of the arrows gives the radius of curvature at each point, which is the reciprocal of the curvature, and the direction of the arrows is the principal unit normal vector at that point.
Rewriting (\ref{dTds}) somewhat, we obtain \begin{equation} \kappa\,ds = d\TT\cdot\NN = -d\NN\cdot\TT \end{equation} where the last equality follows since $\NN\perp\TT$. 1) Thus, the curvature of a curve is a measure of the change in the normal vector along the curve.