You are here: start » book » gdf » surfaces3d
- §1. Curves
- §2. Surfaces
- §3. Examples in 3D
- §4. Curvature
- §5. Curvature in 3D
- §6. Components
- §7. Bianchi Identities
- §8. Geodesic Curvature
- §9. Geodesic Triangles
- §10. Gauss-Bonnet Thm
- §11. The Torus
Examples in Three Dimensions
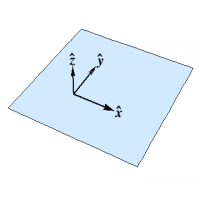
Consider first the $xy$-plane. As shown in Figure 1, we have \begin{align} \ee_1 &= \xhat \\ \ee_2 &= \yhat \\ \nn=\ee_3 &= \zhat \end{align} and of course \begin{equation} d\nn = 0 \end{equation} so that $S$ is the zero matrix, and all of the curvatures are zero.
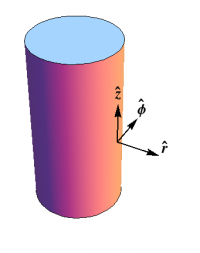
What about a cylinder? As shown in Figure 2, now we have \begin{align} \ee_1 &= \phat \\ \ee_2 &= \zhat \\ \nn=\ee_3 &= \rhat \end{align} and now \begin{equation} d\nn = d\phi\,\phat \end{equation} so that \begin{equation} S = \begin{pmatrix}1/r&0\\0&0\\\end{pmatrix} \end{equation} so that the principal curvatures are $\kappa_1=0$ and $\kappa_2=1/r$. This result should not be a surprise — the cylinder is only curved in one direction. Furthermore, the Gaussian curvature vanishes ($\kappa_1\kappa_2=0$); the cylinder is indeed flat, and can be made by rolling up a piece of paper, without stretching or tearing.
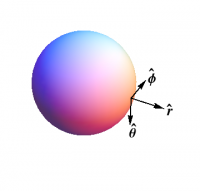
What about a sphere? As shown in Figure 3, in this case we have \begin{align} \ee_1 &= \that \\ \ee_2 &= \phat \\ \nn=\ee_3 &= \rhat \end{align} and now \begin{equation} d\nn = d\theta\,\that + \sin\theta\,d\phi\,\phat \end{equation} which leads to \begin{equation} S = \begin{pmatrix}1/r&0\\0&1/r\\\end{pmatrix} \end{equation} so that the principal curvatures $\kappa_1$ and $\kappa_2$ are both $1/r$. Again, this result should not be a surprise — the sphere has the same curvature in all directions. Furthermore, in this case the Gaussian curvature does not vanish ($\kappa_1\kappa_2=1/r^2$); the sphere can not be made from a piece of paper without stretching or tearing.
These examples lead us to suspect that only the Gaussian curvature is an intrinsic property of a surface. This conjecture turns out to be correct, as we will see shortly. All of the other curvatures — including the curvature of a curve — are extrinsic; they are a property of the way the surface (or curve) sits inside $\RR^3$, but can not be detected by an ant walking along the surface (or curve).