- §1. Curves
- §2. Surfaces
- §3. Examples in 3D
- §4. Curvature
- §5. Curvature in 3D
- §6. Components
- §7. Bianchi Identities
- §8. Geodesic Curvature
- §9. Geodesic Triangles
- §10. Gauss-Bonnet Thm
- §11. The Torus
Geodesic Curvature
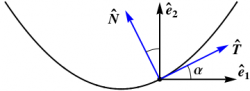
Consider a curve $C$ in a two-dimensional surface $\Sigma$. We will assume Euclidean signature. You can imagine that $\Sigma$ sits inside Euclidean $\RR^3$ if desired, but this is not necessary. Choose an orthonormal basis of vectors $\{\ee_1,\ee_2\}$ as usual. Then, as shown in Figure 1, the unit tangent vector $\TT$ to the curve must satisfy \begin{equation} \TT = \cos\alpha\,\ee_1 + \sin\alpha\,\ee_2 \end{equation} for some angle $\alpha$. Differentiating, we obtain \begin{align} d\TT &= \left( -\sin\alpha\,\ee_1 + \cos\alpha\,\ee_2 \right) \,d\alpha + \cos\alpha\,\omega^2{}_1\,\ee_2 + \sin\alpha\,\omega^1{}_2\,\ee_1 \nonumber\\ &= \left( -\sin\alpha\,\ee_1 + \cos\alpha\,\ee_2 \right) \left( d\alpha - \omega^1{}_2 \right) \end{align} using the symmetry of $\omega_{ij}$ and the fact that in Euclidean signature we can raise and lower indices freely. The vector in parentheses is a unit vector $\NN$ in $\Sigma$ which is orthogonal to the curve, as shown in Figure 1. That is \begin{equation} \NN = -\sin\alpha\,\ee_1 + \cos\alpha\,\ee_2 \end{equation} which can be thought of as $\ee_3\times\TT$, where $\ee_3$ is the normal vector to $\Sigma$ in $\RR^3$. 1) The curvature associated with $\TT$ and $\NN$ is called the geodesic curvature $\kappa_g$ of $C$, and is given by \begin{equation} \kappa_g \,ds = d\TT\cdot\NN = d\alpha - \omega^1{}_2 \end{equation}
A curve with $\kappa_g=0$ is called a geodesic. It is clear from the definition that the geodesics in the plane are straight lines. What are the geodesics on a sphere? A curve on a sphere that does not bend to the left or right is surely a circle, and we can assume without loss of generality that it is a circle of constant latitude. (Why?) The geodesic curvature therefore vanishes if \begin{equation} 0 = d\phat\cdot(-\that) = \cos\theta\,d\phi \end{equation} which is only true at the equator, where $\theta=\pi/2$. Thus, the geodesics on the sphere are great circles, as shown in Figure 2.