The Divergence Theorem relates relates volume integrals to surface integrals of vector fields. Let R be a region in xyz space with surface S. Let n denote the unit normal vector to S pointing in the outward direction. Let F(x,y,z)=<P(x,y,z),Q(x,y,z),R(x,y,z)> be a vector field whose components P, Q, and R have continuous partial derivatives. The Divergence Theorem states:
![]()
Here div F is the divergence of F. There are various technical restrictions on the region R and the surface S; see the references for the details. The theorem is valid for regions bounded by ellipsoids, spheres, and rectangular boxes, for example.
Example
Verify the Divergence Theorem in the case that R is the region satisfying 0<=z<=16-x^2-y^2 and F=<y,x,z>.
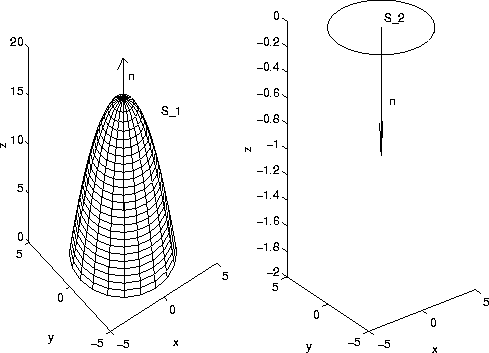
A plot of the paraboloid is z=g(x,y)=16-x^2-y^2 for z>=0 is shown on the left in the figure above. The surface of the region R consists of two pieces. Let us denote the paraboloid by S_1. The intersection of the parabaloid with the z plane is the circle x^2+y^2=16. It follows that that the bottom of R, which we denote by S_2, is the disk x^2+y^2<=16. The surface integral of the vector field is
![]()
where the unit normal vector n points away from the region R.
Let us first consider the surface S_1. The outward normal vector points in the positive z direction. Our previous computation in the flux web page shows that if the normal vector points in the negative direction, then the surface integral equals -128*pi. For a normal vector pointing in the positive z direction the surface integral equals 128*pi.
On the surface S_2, the normal vector points in the negative z direction. In fact, since S_2 lies in the plane z=0, the unit normal vector has x component and y component equal to 0. Hence, <0,0,-1>. On S_2, F=<y,x,z>=<y,x,0>, since S_2 is in the xy plane. It follows that
![]()
Hence, the surface integral on S_2 is 0. The surface integral of F on the entire surface is 128*pi.
Now, let us compute the volume integral. The divergence of F=<P,Q,R >=<y,x,z> is
![]()
It follows that the relevant volume integral is
![]()
The circular symmetry of the region R suggests we convert to cylindrical coordinates. In cartesian coordinates the region R is described by the inequalities 0<=z<=16-x^2-y^2 and 0<=x^2+y^2<=16. In cylindrical coordinates, we have 0<=z<=16-r^2, 0<=r<=4, and 0<=theta<= 2*pi. The above volume integral becomes:
![]()
(There are several ways in the which the integrals can be ordered. However, the z integral must be done before the r integral.) The inner integral is
![]()
(Note that r is held constant). The middle integral with respect to r is
![]()
The outer integral is
![]()
This is the same as the surface integral!
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.