Integration of a function of three variables, w=f(x,y,z), over a three-dimensional region R in xyz-space is called a triple integral and is denoted
![]()
This page contains the following sections:
Triple Integrals in Box-Like Regions
Suppose that R is the box with a<=x<=b, c<=y<=d, and r<=z<=s.
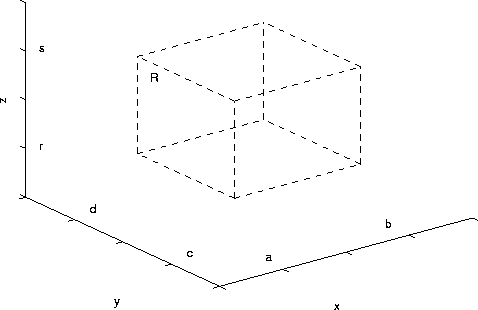
The triple integral is given by
![]()
To compute the iterated integral on the left, one integrates with respect to z first, then y, then x. When one integrates with respect to one variable, all other variables are assumed to be constant. For a box-like region, the integral is independent of the order of integration, assuming f(x,y,z) is continuous. Hence, there are total of 6 ways to order the integrations. For example we can integrate with respect to x, then z, then y. In this case we have
![]()
Consider the following example:
![]()
The inner integral is
![]()
Integrating with respect to z, treating x and y as constants, we obtain
![]()
Note that z has completely disappeared from the expression on the right. The middle integral is with respect to y and x is treated as a constant. We have
![]()
Note that y has disappeared from the expression on the right. The outer integral is with respect to x. We have
![]()
You should verify that the same answer is obtained if the
order of integration is changed.
To get a better understanding of triple integrals let us consider the following example where the triple integral arises in the computation of mass. Suppose that that the region R in xyz-space corresponds to an object and f(x,y,z) is the density per unit volume at the point (x,y,z). If the density is constant, then the mass of the object is the product of the density and the volume of R. If the density varies with position, then we cannot apply this general formula.
We can compute the mass by slicing the R into a bunch of infinitesimal boxes. Consider the box between x and x+dx, y and y+dy, and z and z+dz. Here dx, dy, and dz are infinitesimals. In this small box the density is essentially constant and is equal to f(x,y,z). The mass of the small box is the product of density and volume. The volume of the box is dxdydz. Hence the mass of the the small box is f(x,y,z)dxdydz. The triple integral gives the total mass of the object and is equal to the sum of the masses of all the infinitesimal boxes in R.
Triple integrals also arise in computation of
Triple Integrals in General Regions
We would like to be able to integrate triple integrals for more general regions. General regions are classifed into three types. Suppose that the region R is such that g_1(x,y)<=z<=g_2(x,y), where (x,y) lies in region D in the xy plane, as shown in the figure:

The region D is the projection of R onto the xy plane. The triple integral is given by
![]()
The inner integral
![]()
is with respect to z. The result is a function of x and y. The remainder of the calculation
![]()
is a double integral over the region D in the xy plane.
If the region R is defined such that g_1(x,z)<=y<=g_2(x,z), (x,z) lies in region D in the xz plane, then
![]()
The inner integral is with respect to y. The remainder of the calculation involves a double integral over the region D in the xz plane.
Finally suppose that R is such that g_1(y,z)<=x<=g_2(y,z), where (y,z) lies in a region D in the yz plane, then
![]()
The inner integral is with respect x. The remainder of the calculation involves a double integral over the region D in the yz plane.
Consider the triple integral
![]()
where R is the tetrahedral region bounded by the planes x=0, y=0, z=0 and x+y+z=2 (see figure below).
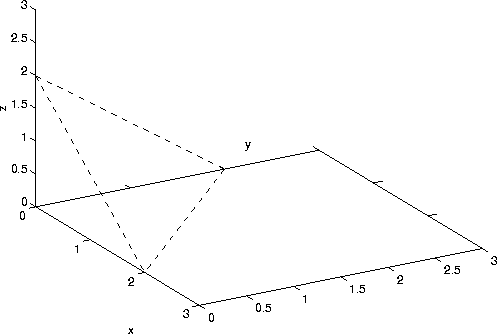
There are several ways to compute the integral. We can rewrite the equation of the plane x+y+z=2 as z=2-x-y. Note that 0<=z=<2-x-y. Hence, we have
![]()
The inner integral is (remember x and y are constants in this integration)
![]()
The projection of the region R onto the xy-plane is the triangle D shown in the figure below:

Hence, we are left with the double integral
![]()
We can also evaluate the double integral by integrating with respect to x first, then y. In this case
![]()
It can be shown that the double integral equals 2/3.
[Vector Calculus Home] [Math 254 Home] [Math 255 Home] [Notation] [References]
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.