Week 2
    Week 3
    Week 4
    Week 5
    Week 6
    Week 7
    Week 8
    Week 9
    Week 10

So far we have seen the wavelike properties of light.  Now we expand this concept to that of particles, like electrons.  Particles will show wavelike behavior in a very similar manner as light.  This effect can be seen through both the traditional double slit and crystal electron diffraction. 

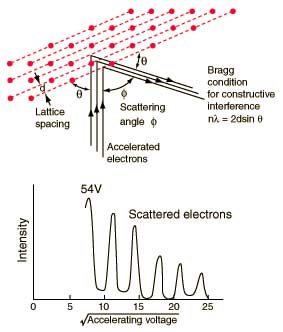
    This experiment was performed shortly after de Broglie's hypothesis of the wave nature of particles.  Incident electrons on a crystalline lattice surface will reflect off that surface.  When they do the resultant wave nature is observed.  With a path length difference in the crystalline lattice the reflected beam exhibits constructive and destructive interference. 

        1.  This experiment was setup and you discovered the second fringe at an angle of Pi/6.  Knowing that the lattice spacing is about 4 angstroms what is the de Broglie wavelength?

The Wave Nature of Matter

    de Broglie proposed a model in which matter exhibits wave like behavior.  This webpage reviews this hypothesis and also explains how this view can be consistent with Bohr's orbital theory of the atom.

        1.  What are the conditions for a wave to fit continuously on a circle?

Exam

    Good luck!

Classical Wave Superposition

    When considering the wave-nature of both particles and light a discussion about wave addition is imperative.  Resultant waves are a superposition of their component waves.  To observe this superposition read through and view this page about wave addition. 

        1.  Using pencil and paper draw two interfering waves of which one is twice the wavelength of the other.   It helps to place one above the other breaking the wave into 10 or more points.  Then add points to create the resultant wave.  

Heisenberg Uncertainty Relationships 

    Heisenberg discovered uncertainty relationships between different characteristics of waves.  When considering the localization of a wave the more localized it becomes the less defined its momentum becomes.  This leads into the famous uncertainty principle that states to more information you have about a particles position the less you have of their momentum.  View this applet to see the comparison between a waves uncertainty of position verses uncertainty of momentum.  The best setting is for a Gaussian wave packet.

        1.  What does /X represent?  What does /P represent?  Draw one of them on a wave.

        2.  If the width of momentum wave function is reduced very small what happens to the position wave function?  How does this correspond to the particles localization and known position?