We move now to three-dimensional Minkowski space, with “squared distance” function given infinitesimally (with $c=1$) by \begin{equation} ds^2 = dx^2 + dy^2 -dt^2 \end{equation} which can of course be positive, zero, or negative. We consider the hyperboloid \begin{equation} x^2 + y^2 - t^2 = -\rho^2 \label{3dmetric} \end{equation} where the radius $\rho$ is a positive constant, and we further restrict ourselves to the branch with $t>0$.

This is the hyperboloid, as shown in Figure 14.1,

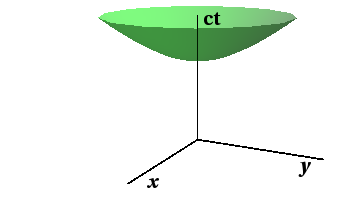Figure 14.1: The hyperboloid in three-dimensional Minkowski space.

We emphasize that, just as with the sphere $x^2+y^2+z^2=\rho^2$, the hyperboloid is a two-dimensional model, even though it lives in three dimensions, since there are only two independent directions at any point on the hyperboloid.

To turn the hyperboloid into a geometric model, we must define its points and lines. Points are, well, points, but what should we count as “straight lines”, henceforth simply called lines? Again, we turn to the sphere for guidance.

The lines on a sphere are the great circles, that is, all possible equators of the sphere. Be careful here; lines of constant longitude are great circles, but lines of constant latitude are not. Lines of constant latitude are not straight! 1) But what corresponds to a “equator on the hyperboloid? A better characterization of lines (great circles) on the sphere is that they are the intersections of the sphere with all possible planes through the origin. This definition carries over unchanged to the hyperboloid.

How do we find the distance between two points? On the sphere, it's easy: Find the angle between the corresponding vectors, and multiply by the radius. How do we find the angle? Use the dot product. This procedure works just as well on the hyperboloid.

Recall the formula (Equation (18) of §5.4) for the dot product of two timelike vectors. If $\uu$ and $\vv$ are vectors from the origin to points $U$ and $V$, respectively, on our hyperboloid, then the distance between $U$ and $V$ is just \begin{equation} d_H(U,V) = -\rho\,\cosh^{-1}\left(\frac{\uu\cdot\vv}{\rho^2}\right) \end{equation} This situation is shown in Figure 14.2,

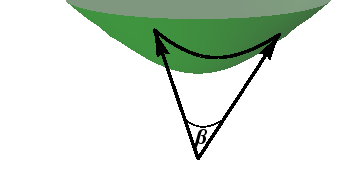Figure 14.2: Using the hyperbolic dot product to measure distance on the hyperboloid.

We can verify this formula in simple cases using coordinates. Introducing natural “hyperboloidal” coordinates, we can write \begin{eqnarray} U &=& (\rho\,\sinh\beta\,\cos\phi,\rho\,\sinh\beta\,\sin\phi,\rho\,\cosh\beta) \label{ucoord}\\ V &=& (\rho\,\sinh\alpha\,\cos\psi,\rho\,\sinh\alpha\,\sin\psi,\rho\,\cosh\alpha) \end{eqnarray} and if $\phi=0=\psi$ we are back in two dimensions, that is, in hyperbola geometry. In this case, the distance between $U$ and $V$ is just \begin{eqnarray} d_H(U,V) &=& \rho\,\cosh^{-1}(-\sinh\alpha\sinh\beta+\cosh\alpha\cosh\beta) \nonumber\\ &=& \rho\,\cosh^{-1}(\cosh(\beta-\alpha)) \\ &=& \rho\,(\beta-\alpha) \nonumber \end{eqnarray} as expected.

Infinitesimal distance on the hyperboloid is obtained by rewriting ($\ref{3dmetric}$) in hyperboloidal coordinates ($\rho$,$\beta$,$\phi$). We obtain \begin{equation} ds^2 = \rho^2\,d\beta^2 + \rho^2\,\sinh^2\beta\,d\phi^2 - d\rho^2 \end{equation} which is not at all surprising if one recalls the similar computation in spherical coordinates. Since $\rho=\hbox{constant}$ on the hyperboloid, infinitesimal distance on the hyperboloid is given by \begin{equation} ds^2 = \rho^2\,d\beta^2 + \rho^2\,\sinh^2\beta\,d\phi^2 \label{Hmetric} \end{equation} which again recalls the line element on a sphere.

It is important to note that even though we used Minkowski space in our construction, with its indefinite distance function, the end result is a positive-definite (Riemannian) notion of distance. There are no light beams within the hyperboloid.