Each of the preceding models of hyperbolic geometry has its advantages and disadvantages. The two Poincaré models are conformal, so angles are easy to measure, but lines are not obvious. Lines in the Klein model are obvious, but angles are hard to measure. And for all its similarity with the sphere, in the hyperboloid model neither lines nor angles are easy to determine. Furthermore, none of these models exists in ordinary (three-dimensional) Euclidean space. Perhaps that is no surprise; after all, why should a model for hyperbolic geometry be constructible within Euclidean geometry? The surprise is that this is indeed possible, as we now show.

The pseudosphere is most simply related to the Poincaré half-plane, which we described in terms of dimensionless variables ($X$,$Y$) in §14.3. We introduce new variables $\alpha$ and $\theta$ via \begin{eqnarray} \sin\alpha &=& \frac{1}{Y} \\ \theta &=& X \end{eqnarray} and compute \begin{equation} ds^2 = \rho^2\>\frac{dX^2+dY^2}{Y^2} = \rho^2 \left( \cot^2\alpha\,d\alpha^2 + \sin^2\alpha\,d\theta^2 \right) \label{hptops} \end{equation} We claim this line element describes a surface of revolution in Euclidean space!

A surface of revolution in ordinary (3-dimensional) Euclidean space can be described in cylindrical coordinates ($r$,$\theta$,$z$) by specifying $r$ and $z$ in terms of some parameter $\alpha$. The line element on the surface is then \begin{equation} ds^2 = dr^2 + r^2\,d\theta^2 + dz^2 = \left( \left(\frac{dr}{d\alpha}\right)^2 + \left(\frac{dz}{d\alpha}\right)^2 \right) d\alpha^2 + r^2\,d\theta^2 \label{rev} \end{equation} Comparing ($\ref{rev}$) with ($\ref{hptops}$), we must have \begin{equation} r = \rho\,\sin\alpha \label{rtractrix} \end{equation} and therefore \begin{equation} \left(\frac{dz}{d\alpha}\right)^2 = \rho^2\,\cot^2\alpha - \rho^2\,\cos^2\alpha = \rho^2\,\frac{\cos^4\alpha}{\sin^2\alpha} \end{equation} One solution of this differential equation is \begin{equation} z = -\rho\,\cos\alpha - \rho\,\ln\tan\left(\frac{\alpha}{2}\right) \label{ztractrix} \end{equation}

 
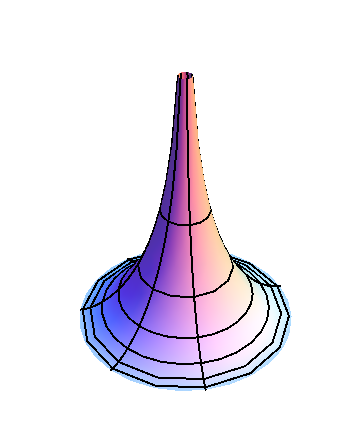
Figure 14.7: The first figure shows the tractrix, whose surface of revolution is the pseudosphere shown alongside.

Equations ($\ref{rtractrix}$) and ($\ref{ztractrix}$) with $\alpha\in[0,\pi/2]$ describe a curve known as a tractrix, as shown on the left in Figure 14.7. The pseudosphere is the surface of revolution obtained by rotating the tractrix about the $z$-axis, as shown on the right in Figure 14.8, We can also embed the pseudosphere in one of the other models of hyperbolic geometry, as shown for the hyperboloid in Figure 14.9. The periodicity in $\theta$ requires that we identify the edges as shown in the figure; the pseudosphere can be thought of as a “rolled-up” piece of the hyperboloid. We can think of the horizontal slices of the pseudosphere as circles centered at infinity (the tip of the pseudosphere), with infinite radius (the length from the center, as measured along the pseudosphere).

What is so special about the pseudosphere?

A Euclidean plane has the property that it is the same everywhere, and in in all directions. Thus, a piece of cardboard can be placed on a flat table anywhere, and in any orientation, and will fit snugly. We describe this by saying that the table is flat (as is the piece of cardboard); its curvature is zero. A sphere has the same property: Peel an orange, and you can put a piece of the peel back anywhere on the orange, in any orientation, and it will fit snugly. The orange has constant (positive) curvature. The hyperboloid also has this property; it has constant negative curvature. If you could peel it, the peel would fit snugly anywhere, and in any orientation. But the hyperboloid lives in Minkowski space, so this property seems to be far removed from reality.

Yet we have succeeded in building a model of the hyperboloid in Euclidean space. This model has exactly the same intrinsic properties as any other model of hyperbolic geometry, including the hyperboloid. This means that if you were to build a pseudosphere, and then “peel” it, 1) you could take that piece of peel and put it anywhere, in any orientation, and it would fit snugly, without tearing or stretching.

This is indeed remarkable.

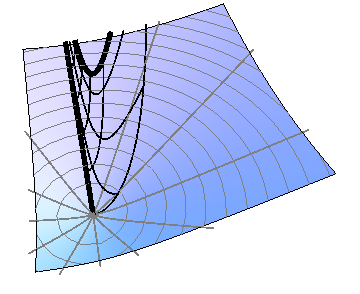Figure 14.8: Embedding the pseudosphere in the hyperboloid. The heavy lines are to be identified.