In Euclidean geometry, (squared!) distances can be described by taking the dot product of a vector with itself. Denoting the unit vectors in the $x$ and $y$ directions by $\xhat$ and $\yhat$, respectively, then the vector from the origin to the point $(x,y)$ is just \begin{equation} \rr = x\,\xhat + y\,\yhat \end{equation} whose (squared) length is just \begin{equation} |\rr|^2 = \rr\cdot\rr = x^2 + y^2 \end{equation}

It is straightforward to generalize this to hyperbola geometry. Denote the unit vectors in the $t$ and $x$ directions by $\that$ and $\xhat$. 1) Then the (Lorentzian) dot product can be defined by the requirement that this be an orthonormal basis, in the sense that \begin{eqnarray} \xhat\cdot\xhat &=& 1 \\ \that\cdot\that &=& -1 \\ \xhat\cdot\that &=& 0 \end{eqnarray} Any point ($x$, $ct$) in spacetime can thus be identified with the vector \begin{equation} \rr = x\,\xhat + ct\,\that \end{equation} from the origin to that point, whose “squared length” is just the “squared distance” from the origin, namely \begin{equation} |\rr|^2 = \rr\cdot\rr = x^2 - \csq t^2 \end{equation}

One of the fundamental properties of the Euclidean dot product is that \begin{equation} \uu\cdot\vv = |\uu| |\vv| \cos\theta \end{equation} where $\theta$ is the (smallest) angle between the directions of $\uu$ and $\vv$. This relationship between the dot product and projections of one vector along another can in fact be used to define the dot product. What happens in hyperbola geometry?

First of all, the dot product can be used to define right angles: Two vectors $\uu$ and $\vv$ are said to be orthogonal (or perpendicular) precisely when their dot product is zero, that is \begin{equation} \uu\perp\vv \Longleftrightarrow \uu\cdot\vv = 0 \end{equation} We will adopt this definition unchanged in hyperbola geometry.

When are $\uu$ and $\vv$ perpendicular? Assume first that $\uu$ is spacelike. We can assume without loss of generality that $\uu$ is a unit vector, in which case it takes the form \begin{equation} \uu = \cosh\alpha \,\xhat + \sinh\alpha \,\that \end{equation} What vectors are perpendicular to $\uu$? One such vector is \begin{equation} \vv = \sinh\alpha \,\xhat + \cosh\alpha \,\that \end{equation} and it is easy to check that all other solutions are multiples of this one. Note that $\vv$ is timelike! Had we assumed instead that $\vv$ were timelike, we would merely have interchanged the roles of $\uu$ and $\vv$.

Furthermore, $\uu$ and $\vv$ are just the space and time axes, respectively, of an observer moving with speed $\vc=\tanh\alpha$. So orthogonal directions correspond precisely to the coordinate axes of some observer.

What if $\uu$ is lightlike? It is a peculiarity of Lorentzian (hyperbola) geometry that there are nonzero vectors of length zero. But since the dot product of a vector with itself gives its squared length, having length zero means that lightlike vectors are perpendicular to themselves!

We can finally define the length of a vector $\vv$ by \begin{equation} |\vv| = \sqrt{|\vv\cdot\vv|} \end{equation} If $\vv$ is spacelike we can write \begin{equation} \vv = \pm |\vv| (\cosh\alpha \,\xhat + \sinh\alpha \,\that) \end{equation} while if $\vv$ is timelike we can write \begin{equation} \vv = \pm |\vv| (\sinh\alpha \,\xhat + \cosh\alpha \,\that) \end{equation} If $\vv$ is lightlike, $|\vv|=0$, so no such expression exists. Rather, \begin{equation} \vv = a\, (\xhat \pm \that) \end{equation} for some constant $a$.

The above argument shows that timelike vectors can only be perpendicular to spacelike vectors, and vice versa. We will also say in this case that the vectors form a right angle. Recall that hyperbolic angles were defined along hyperbolas of the form $x^2-\csq t^2 = \rho^2$, hence only exist (as originally defined) between spacelike directions! It is straightforward to extend this to timelike directions using the hyperbola $x^2-\csq t^2=-\rho^2$; this was implicitly done when drawing Figure 4.2. But there is no hyperbola relating timelike directions to spacelike ones. Thus, a “right angle” isn't an angle at all!

A right triangle is one which contains a right angle. By the above discussion, one of the legs of such a triangle must be spacelike, and the other timelike. Consider first the case where the hypotenuse is either spacelike or timelike. The only hyperbolic angle in such a triangle is the one between the hypotenuse and the leg of the same type, that is between the two timelike sides if the hypotenuse is timelike, and between the two spacelike sides if the hypotenuse is spacelike. Several such hyperbolic right triangles are shown in Figure 5.4. It is also possible for the hypotenuse to be null, as shown in Figure 5.5. Such triangles do not have any hyperbolic angles! Finally, as shown in the last two diagrams in Figure 5.5, right angles do not always look like right angles! Can you combine these ideas, and draw a 3–4–5 triangle, none of whose sides are horizontal or vertical?

 
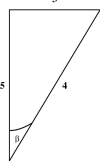
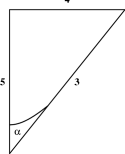
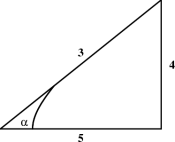
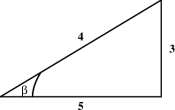
Figure 5.4: Some hyperbolic right triangles.

 
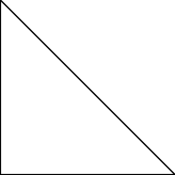
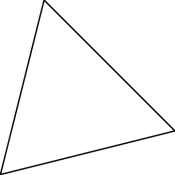
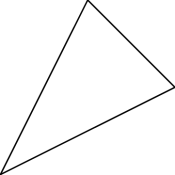
Figure 5.5: More hyperbolic right triangles. The right angle is on the left!

What happens if we take the dot product between two spacelike vectors? We can assume without loss of generality that one vector is parallel to the $x$ axis, in which case we have \begin{eqnarray} \uu &=& |\uu| \,\xhat \\ \vv &=& |\vv| (\cosh\alpha \,\xhat + \sinh\alpha \,\that) \end{eqnarray} so that the dot product satisfies \begin{equation} \uu\cdot\vv = |\uu| |\vv| \cosh\alpha \end{equation} % What happens if both vectors are timelike? The above argument still works, except that the roles of $\xhat$ and $\that$ must be interchanged, resulting in \begin{equation} \uu\cdot\vv = - |\uu| |\vv| \cosh\alpha \label{tdot} \end{equation} In both cases, note that $|\vv|\cosh\alpha$ is the projection of $\vv$ along $\uu$; see Figure 5.6.

 
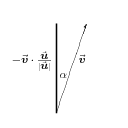
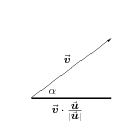
Figure 5.6: Hyperbolic projections between two timelike vectors, or between two spacelike vectors. In both cases, $\uu$ points along the heavy line.

But what happens if we take the dot product between a timelike vector and a spacelike vector? We can again assume without loss of generality that the spacelike vector is parallel to the $x$ axis, so that \begin{eqnarray} \uu &=& |\uu| \,\xhat \\ \vv &=& |\vv| (\sinh\alpha \,\xhat + \cosh\alpha \,\that) \end{eqnarray} The dot product now satisfies \begin{equation} \uu\cdot\vv = |\uu| |\vv| \sinh\alpha \end{equation} At first sight, this is something new. But note from the first drawing in Figure 5.7 that $\vv\sinh\alpha$ is just the projection of $\vv$ along $\uu$! The new feature here is that we can't define the angle between a timelike direction and a spacelike direction. The only angle in the triangle which is defined is the one shown! 2)

 
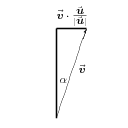
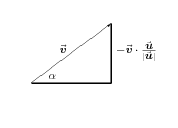
Figure 5.7: Hyperbolic projections between timelike and spacelike vectors. The direction of $\uu$ in each case is the reverse of that shown in Figure 5.6, namely horizontally in the first drawing, and vertically in the second.