- §1. Extending Schwarzschild
- §2. Kruskal Geometry
- §3. Penrose Diagrams
- §4. Charged Black Holes
- §5. Rotating Black Holes
Extending Schwarzschild Geometry
We now apply the same technique used in Chapter in § Rindler, to extend the Rindler geometry to the Schwarzschild geometry. Consider a radial light beam, so that $d\phi=0$ (and as usual $\theta=\pi/2$). Then the line element becomes
\begin{equation} ds^2 = -\left(1-\frac{2m}{r}\right)\,dt^2 + \frac{dr^2}{1-\frac{2m}{r}} = -\left(1-\frac{2m}{r}\right) \left( dt^2 - \frac{dr^2}{\left(1-\frac{2m}{r}\right)^2} \right) \end{equation} which we can factor as \begin{equation} ds^2 = -\left(1-\frac{2m}{r}\right) \left( dt - \frac{dr}{1-\frac{2m}{r}} \right) \left( dt + \frac{dr}{1-\frac{2m}{r}} \right) \label{schwf} \end{equation}
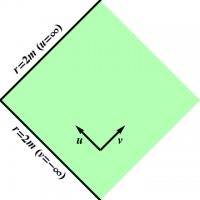
This motivates the definition \begin{align} du &= dt - \frac{dr}{1-\frac{2m}{r}} \\ dv &= dt + \frac{dr}{1-\frac{2m}{r}} \end{align} which we can integrate to obtain \begin{align} \frac{v-u}{2} &= \int \frac{dr}{1-\frac{2m}{r}} \nonumber\\ &= \int \left( 1 + \frac{1}{\frac{r}{2m}-1} \right) \, dr \nonumber\\ &= r + 2m \ln\left(\frac{r}{2m}-1\right) \label{ruv} \end{align} Expression (\ref{ruv}) relating $r$ to $u$ and $v$ is badly behaved at $r=2m$. However, for $r>2m$, the coordinates $(u,v)$ behave much like their namesakes in Rindler geometry, as shown in Figure 1 (compare Figure 1 of § Extending Rindler Geometry). Furthermore, we can extend the geometry across the apparent singularity at $r=2m$ if we exponentiate, which yields \begin{equation} e^{(v-u)/4m} = e^{r/2m} \left(\frac{r}{2m}-1\right) = e^{r/2m} \frac{r}{2m} \left(1-\frac{2m}{r}\right) \label{ruvexp} \end{equation} Inserting (\ref{ruvexp}) back into the factored line element ($\ref{schwf}$) leads to \begin{align} ds^2 &= - \frac{2m}{r} e^{-r/2m} e^{(v-u)/4m} \,du \,dv \nonumber\\ &= - \frac{32m^3}{r} e^{-r/2m} \left(e^{-u/4m} \,\frac{du}{4m} \right) \left( e^{v/4m} \,\frac{dv}{4m} \right) \nonumber\\ &= - \frac{32m^3}{r} e^{-r/2m} \,dU \,dV \label{schwmetUV} \end{align} where \begin{align} U &= -e^{-u/4m} \\ V &= e^{v/4m} \end{align} The line element (\ref{schwmetUV}) is perfectly well behaved at $r=2m$! The coordinates $\{U,V,\theta,\phi\}$ are known as (double-null) Kruskal-Szekeres coordinates. The radial coordinate $r$ can be expressed (implicitly) in terms of $U$ and $V$ via \begin{equation} UV = - e^{(v-u)/4m} = e^{r/2m} \left(1-\frac{r}{2m}\right) \end{equation} Finally, orthogonal coordinates $\{T,X\}$ can be introduced if desired by writing \begin{align} U &= T-X \\ V &= T+X \end{align}