- §1. Extending Schwarzschild
- §2. Kruskal Geometry
- §3. Penrose Diagrams
- §4. Charged Black Holes
- §5. Rotating Black Holes
Kruskal Geometry
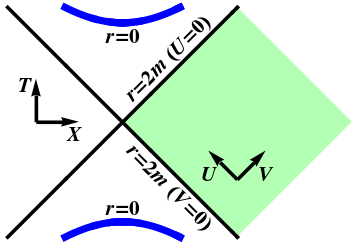
Since Kruskal-Szekeres coordinates $U$ and $V$ are well-defined at $r=2m$, we can use them to extend Schwarzschild geometry to $r<2m$. The maximally extended Schwarzschild geometry, also called the Kruskal geometry is obtained by extending the domains of $U$, $V$ as much as possible, and is shown in Figure 1.
Since \begin{equation} UV = e^{r/2m} \left(1-\frac{r}{2m}\right) \end{equation} we see that $U=0$ or $V=0$ where $r=2m$, and the original Schwarzschild geometry corresponds to the quadrant $U<0$, $V>0$. We would like to consider all possible values of $U$ and $V$, but what values are allowed? Kruskal-Szekeres coordinates are badly behaved at $r=0$, which turns out to be a true singularity, since the curvature blows up there. We therefore require $r>0$, which implies that \begin{equation} UV<1 \end{equation} Thus, the $U$ and $V$ axes correspond to the horizons at $r=2m$, and the singularities at $r=0$ correspond to $UV=1$, and are shown as thick lines. The shaded region represents the original Schwarzschild region, with $r>2m$.
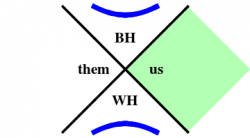
Figure 1 reveals the true nature of the Schwarzschild black hole. The $U$ and $V$ axes divide the Kruskal geometry into four regions, as shown in Figure 2. Since the angular coordinates $\theta$ and $\phi$ have been suppressed, each point in this diagram represents a sphere of radius $r$. The original Schwarzschild region is the righthand quadrant, which is bordered by two horizons, one in the past, and the other in the future. Since the horizons at $U=0$ and $V=0$ are lightlike, nothing can escape from the top quadrant; this region describes (the interior of a) black hole. Once you're in this region, you can only move upward in the diagram (forward in time), at less than the speed of light. Not even a beam of light that starts in the black hole region can escape to the outside ($r>2m$), where we could see it! There is also a time-reversed copy of this region in the bottom quadrant, from which everything must eventually escape; this region describes a white hole. Finally, there is a second Schwarzschild region on the left, which however can not communicate with the original Schwarzschild region on the right. For this reason, the two Schwarzschild regions are often referred to as “us” and “them”.
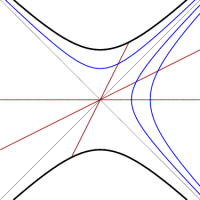
Lines of constant $r$ (hyperbolas) and $t$ (straight lines) are shown in Figure 3. This diagram should remind you of Rindler geometry! Shell observers at constant $r$ must accelerate in order to avoid falling into the black hole; surfaces of constant $t$ must be orthogonal to the worldlines of such observers. The same description holds inside the black hole region, with $r<2m$, but the roles of $r$ and $t$ have been reversed: $r$ is now time. Moving into the future thus forces $r$ to decrease; it is not possible to avoid reaching the singularity at $r=0$, and it turns out that a falling object does so in finite proper time. There is no escape from a black hole!
What does the Kruskal geometry look like at any instant of time? Since surfaces of constant $t$ all meet at the origin, they do not represent a good global notion of “constant time”. (This notion of “time” would also run backward in the left-hand quadrant!) We therefore analyze the geometry of surfaces of constant $T$, as shown in Figure 4. Start at the bottom, with the line $T=0$. Each point on this line represents a sphere, and it is comforting to think of spheres of different radii as lying inside each other. Such a description works fine far away from the horizon, but the spheres on the left are unrelated to the spheres on the right. Imagine therefore two sheets of paper, on which concentric circles (representing spheres) are drawn. For $r\gg 2m$, the geometry is indeed flat. But there are no spheres on this surface with $r<2m$, and in fact the two regions come together at $r=2m$. This situation can be modeled by connecting the two pieces of paper along a tube, whose minimum radius is $2m$; the two Schwarzschild regions are connected by a wormhole, as shown in the bottom diagram in Figure 5. Although this figure is drawn in three dimensions, it must be emphasized that the vertical direction in the figure is not a physical direction in Kruskal geometry. Such diagrams are called embedding diagrams, and can be quite useful for visualization, so long as one remembers that only the surface itself corresponds to (part of) Kruskal geometry.
Before incorporating such wormholes into your favorite science fiction scenario, let's explore what happens as $T$ increases. Successive surfaces with $T$ constant are shown in Figure 4, and the topology of these surfaces is shown in Figure 5. One angular coordinate is suppressed; each circle is really a sphere of constant radius. In each case, the mostly flat region at the top of the figure corresponds to the right-hand region (“us”), and the bottom to the left-hand region (“them”). As $T$ increases (up the page), the minimum radius on the surface decreases below $2m$. Eventually, the minimum radius of the wormhole reaches $0$, after which it pinches off, after which the two Schwarzschild regions are disconnected from each other. By following a timelike path in Kruskal geometry, it is easy to see that a Kruskal wormhole pinches off before it is possible to traverse it from one Schwarzschild region to the other; it is not possible to travel through a Kruskal wormhole.
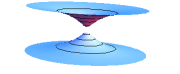
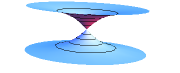
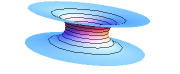
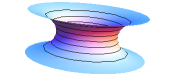
Figure 5: The topology of surfaces of constant $T$ in the Kruskal geometry,
corresponding to the cases shown in Figure 4.