Figure 7: A hyperbolic triangle showing the hyperbolic angle between shell observers and rain observers.

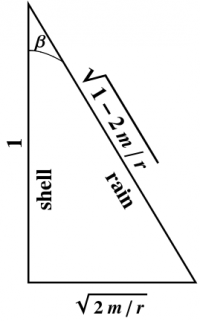
We digress briefly to introduce “rain” coordinates adapted to freely falling observers who start from rest at $r=\infty$, each of whom moves along a geodesic as described in the preceding section. As shown there, a shell observer sees such observers fall past them with speed \begin{equation} \tanh\beta = -\sqrt{\frac{2m}{r}} \end{equation} Drawing a right triangle to these proportions, as shown in Figure 6, or using the algebraic relationships between the hyperbolic trig functions, we find \begin{align} \cosh\beta &= \frac{1}{\sqrt{1-\frac{2m}{r}}} \label{rcosh}\\ \sinh\beta &= -\frac{\sqrt{\frac{2m}{r}}}{\sqrt{1-\frac{2m}{r}}} \label{rsinh} \end{align}

The orthonormal basis of 1-forms associated with shell observers is \begin{align} \sigma^t &= \sqrt{1-\frac{2m}{r}}\,dt \\ \sigma^r &= \frac{dr}{\sqrt{1-\frac{2m}{r}}} \\ \sigma^\theta &= r\,d\theta \\ \sigma^\phi &= r\,\sin\theta\,d\phi \end{align} This basis is associated with shell observers, because spatial distances measured by such observers are given by integrating $\sigma^r$ (with $t$ held constant, and hence with $\sigma^t=0$), and the time intervals measured by such observers are given by integrating $\sigma^t$ (with $r$ held constant, so that $\sigma^r=0$).

We can obtain an orthonormal basis of 1-forms associated with freely falling observers by using a Lorentz transformation to “rotate” the shell basis to one traveling at the correct speed. We thus define \begin{align} \sigma^T &= \sigma^t\cosh\beta - \sigma^r\sinh\beta \\ \sigma^R &= \sigma^r\cosh\beta - \sigma^t\sinh\beta \label{Rform} \end{align}

Inserting the above expressions (\ref{rcosh}) and (\ref{rsinh}) for $\cosh\beta$ and $\sinh\beta$, we find \begin{align} \sigma^T &= dt + \frac{\sqrt{\frac{2m}{r}}}{1-\frac{2m}{r}} \>dr \\ \sigma^R &= \frac{dr}{1-\frac{2m}{r}} + \sqrt{\frac{2m}{r}} \>dt \end{align} The first of these equations can be integrated directly, yielding \begin{equation} T = t + \int \frac{\sqrt{\frac{2m}{r}}}{1-\frac{2m}{r}} \>dr = t + 4m \left( \sqrt{\frac{r}{2m}} + \frac12\ln\left| \frac{\sqrt{\frac{r}{2m}}-1}{\sqrt{\frac{r}{2m}}+1} \right| \right) \end{equation}

Figure 8: The relationship between shell observers and rain observers.

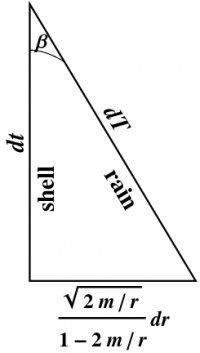
Thus, \begin{equation} \sigma^T = dT \end{equation} To see that this basis is indeed associated with freely falling observers, set $\sigma^R=0$ in (\ref{Rform}) (“standing still”), which implies that $\tanh\beta=\sigma^r/\sigma^t$ as desired. Furthermore, if $\sigma^R=0$, $\sigma^T=dT$ measures proper time. Thus, $T$ is the proper time of the freely falling observers. We therefore refer to $\{\sigma^T,\sigma^R\}$ as the “rain” frame. 1) The relationship between rain coordinates and our original “shell” coordinates is shown in Figure 7.

After dividing through by $\sqrt{2m/r}$, it is also possible to integrate the second equation, resulting in an orthogonal coordinate system. However, since $r$ has geometric meaning it is more common to retain it as a coordinate. We can nevertheless replace $dt$ by $dT$ in $\sigma^R$, resulting in \begin{equation} \sigma^R = dr + \sqrt{\frac{2m}{r}}\>dT \end{equation} We can now write the line element in “rain” coordinates as \begin{align} ds^2 &= -(\sigma^t)^2 + (\sigma^r)^2 + (\sigma^\theta)^2 + (\sigma^\phi)^2 \nonumber\\ &= -(\sigma^T)^2 + (\sigma^R)^2 + (\sigma^\theta)^2 + (\sigma^\phi)^2 \nonumber\\ &= -dT^2 + \left(dr+\sqrt{\frac{2m}{r}}\>dT\right)^2 + r^2\,d\theta^2 + r^2\,\sin^2\theta\,d\phi^2 \nonumber\\ &= - \left(1-\frac{2m}{r}\right)\>dT^2 + 2\sqrt{\frac{2m}{r}}\>dT\,dr \nonumber\\ & \qquad {}+ dr^2 + r^2\,d\theta^2 + r^2\,\sin^2\theta\,d\phi^2 \end{align} This line element has several unexpected properties:

• The line element is perfectly well-defined as $r$ approaches $2m$.
• The $T$ direction is not orthogonal to the $r$ direction.
• Surfaces with $T$ constant ($dT=0$) are flat! (The line element reduces to that of Euclidean 3-space, in spherical coordinates.)
• The surface $r=2m$ is lightlike! ($T$ is a lightlike direction there.)

Since the line element is well-behaved at $r=2m$, we can use it to ask what happens to a beam of light crossing the horizon. For a beam of light, we have $ds^2=0$, and hence \begin{equation} dT^2 = \left( dr + \sqrt{\frac{2m}{r}}\>dT \right)^2 \end{equation} so that \begin{equation} dT = \pm\left( dr + \sqrt{\frac{2m}{r}}\>dT \right) \end{equation} or equivalently \begin{equation} \left( 1\mp\sqrt{\frac{2m}{r}} \right)\>dT = \pm dr \end{equation} so that \begin{equation} \frac{dr}{dT} = \pm \left( 1\mp\sqrt{\frac{2m}{r}} \right) \end{equation} We expect $dr/dT>0$ for an outgoing beam of light, and $dr/dT<0$ for an ingoing beam of light. But if $r<2m$ we have $dr/dT<0$ in both cases! Light can not escape from $r<2m$! As we will see in more detail in § Black Holes, this is a black hole.