- §1. The Schwarzschild Metric
- §2. Schwarzschild Geometry
- §3. The Geodesic Equation
- §4. Newtonian Motion
- §5. Orbits
- §6. Circular Orbits
- §7. Null Orbits
- §8. Radial Geodesics
- §9. Rain Coordinates
- §10. Schwarzschild Observers
Orbits
In § Newtonian Motion and § Schwarzschild Geodesics, we have seen that the trajectory of an object moving in the gravitational field of a point mass is controlled by the object's energy per unit mass ($e=E/M$), and its angular momentum per unit mass ($\ell=L/M$). In the Newtonian case, we have \begin{equation} \frac12 \dot{r}^2 = e - \left(-\frac{m}{r} + \frac{\ell^2}{2r^2}\right) \label{rdotn} \end{equation} from Equation (11) of § Newtonian Motion (where we have set $G=1$), and in the relativistic case we have \begin{equation} \frac12\dot{r}^2 = \frac{e^2 - 1}{2} - \left( -\frac{m}{r} + \frac{\ell^2}{2r^2} -\frac{m\ell^2}{r^3} \right) \label{rdote} \end{equation} from Equation (16) of § Schwarzschild Geodesics. Both of these equations take the form \begin{equation} \frac12\dot{r}^2 = \hbox{constant} - V \end{equation} where the constant depends on the energy $e$, and the potential $V$ depends on both the mass $m$ of the source and the angular momentum $\ell$ of the object.
In the Newtonian case (\ref{rdotn}), the right-hand side is quadratic in $r$, and it is straightforward to solve this ordinary differential equation, typically by first substituting $u=1/r$. The solutions, of course, are conic sections. In the relativistic case (\ref{rdote}), the right-hand side is cubic in $r$. This differential equation can also be solved in closed form, but the solution requires elliptic functions as well as solving for the zeros of the cubic polynomial. Rather than present the messy details of such a computation, we give an alternative analysis here, then consider special cases such as circular and radial trajectories in subsequent sections.
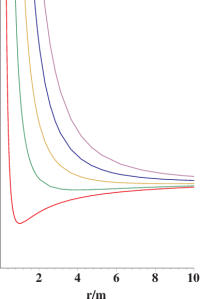
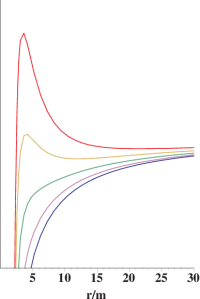
A standard method for analyzing the resulting trajectories is to plot $V$ as a function of $r$ for various values of $\ell$ and $m$, then draw horizontal lines corresponding to the value of the constant, which depends only on the energy $e$. The points where these lines intersect the graph of $V$ represent radii at which $\dot{r}=0$; points on the line which lie above the graph have $|\dot{r}|>0$, while points below the graph are unphysical. Plots of the potential $V$ for various values of $\ell/m$ are shown in Figure 1 (Newtonian) and Figure 2 (relativistic).
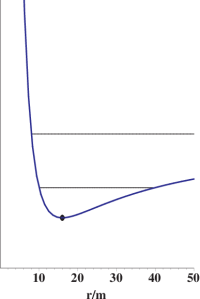
A typical Newtonian example is given in Figure 3. The potential $V$ has a single extremum, namely a global minimum at \begin{equation} \frac{r}{m} = \frac{\ell^2}{m^2} \end{equation} which corresponds to a stable circular orbit, as indicated by the dot in Figure 3. With a little more energy, the object travels back and forth between a minimum radius and maximum radius; these are bound orbits, which turn out to be ellipses. These orbits are represented by the lower horizontal line in Figure 3. Finally, with enough energy, the object reaches a minimum radius, then turns around and never comes back; this is a “slingshot” orbit, and is represented by the upper horizontal line in Figure 3. 1)
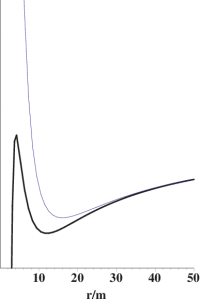
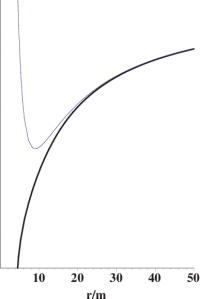
Newtonian (thin line) and relativistic (heavy line) potentials with $\ell=4m$ are shown superimposed in Figure 4, to emphasize that these potentials agree far from the source ($r\gg m$). However, for small $r$ the potentials are dramatically different. In particular there is another extremum in the relativistic case, which is a local maximum, and hence corresponds to an unstable circular orbit. Furthermore, with enough energy it is now possible to reach $r=0$ even with nonzero angular momentum, which is impossible in the Newtonian case.
Finally, since the condition for the location of extrema of $V$ is quadratic in the relativistic case, there are parameter values for which no such extrema exist. For example, as shown in Figure 5, if $\ell=3m$, the relativistic potential (heavy line) has neither minima nor maxima, and no circular orbits exist. As we will see below, this implies that in the relativistic case there are radii at which one can not orbit (without a boost from rocket engines), whereas in the Newtonian case one can always do so for suitable values of $e$ and $\ell$.