We repeat the computations in the previous section for lightlike orbits. We still have \begin{align} \ell &= \Pvec\cdot\vv = r^2 \dot\phi \\ e &= -\Tvec\cdot\vv = \left(1-\frac{2m}{r}\right)\dot{t} \end{align} but now \begin{equation} 0 = \left(1-\frac{2m}{r}\right)\,\dot{t}^2 - \frac{\dot{r}^2}{1-\frac{2m}{r}} - r^2\,\dot\phi^2 \end{equation} which leads to \begin{equation} \dot{r}^2 = e^2 - \left(1-\frac{2m}{r}\right)\frac{\ell^2}{r^2} \label{nullgeo} \end{equation}

But wait a minute. What do these symbols mean? What does the “dot” refer to if $d\tau=0$? And how are we supposed to interpret “energy per unit mass” ($e$), or “angular momentum per unit mass” ($\ell$)?

To answer the first question, we note that the geodesic equation, $\dot\vv=0$, automatically implies that \begin{equation} \left(|\vv|^2\right)\Dot = 2 \vv\cdot\dot\vv = 0 \end{equation} Thus, the magnitude of the “velocity” vector $\vv=\dot\rr$ is constant; geodesics are curves of “constant speed”. In the timelike case, we can choose the parameter to be proper time $\tau$, and these names are reasonable. In the spacelike case, we can choose the parameter to be proper distance, and everything goes through as before, although the terms “velocity” and “speed” do not accurately reflect the physics. In both of these cases, it is part of the geodesic equation that we must choose the parameter in this way, up to a constant factor (change in units, e.g. between minutes and seconds) and an additive constant (shift in origin, e.g. between time zones). A geodesic is not merely a set of points, but rather a set of points traversed in uniform fashion. The allowable parameters are called affine parameters; two affine parameters $u$, $v$ are related by a linear equation of the form \begin{equation} v = a u + b \end{equation} for some constants $a$ and $b$.

Thus, the choice of which affine parameter to use is not formally a part of the geodesic equation, but the requirement that one use an affine parameter most definitely is. For timelike geodesics, we make the conventional choice to use proper time, and for spacelike geodesics we make the conventional choice to use proper distance (arclength), but for null geodesics there is no analogous preferred choice of affine parameter. The “dot” therefore refers to any choice of affine parameter along null geodesics.

Figure 1: Lightlike momentum as a limit of timelike momenta.

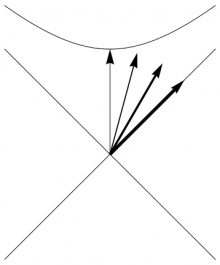
As for the second question, this is a common problem when attempting to interpret the lightlike case as some sort of limit of timelike directions, since the “rapidity” parameter $\beta$ in $\frac{v}{c}=\tanh\beta$ approaches $\infty$ as $v$ approaches $c$. The correct resolution, as shown in Figure 1, is that we should be looking at the 4-momentum \begin{equation} \pp = M\,\vv \end{equation} rather than the 4-velocity $\vv$. The quantities on the right, $M$ and $\vv$, are separately poorly defined for lightlike objects (such as photons), but $\pp$ turns out to be a well-defined physical property of such massless objects.

Thus, for null geodesics, we would be better off defining the constants of the motion to be 1) \begin{align} L &= \Pvec\cdot\pp \\ E &= -\Tvec\cdot\pp \end{align} where $L$ really is the angular momentum, and $E$ the energy, associated with the lightlike object. We can, however, use the freedom in the affine parameter to replace $e$ and $\ell$ in (\ref{nullgeo}) by $E$ and $L$, respectively.

Returning to (\ref{nullgeo}) and differentiating, we recover the ($r$-component of the) full, second-order geodesic equation in the form \begin{equation} \ddot{r} = \frac{L^2}{r^3}\left(1-\frac{3m}{r}\right) \end{equation} and, as before, this equation still holds when $\dot{r}=0$. Thus, the only lightlike circular orbit occurs at $r=3m$. Equation (\ref{nullgeo}) further implies that $L^2/E^2=27m^2$ on such an orbit.