The Jacobian for Polar and Spherical Coordinates

We first compute the Jacobian for the change of variables from Cartesian coordinates to polar coordinates.

Recall that

Hence,

The Jacobian is

Correction There is a typo in this last formula for J. The (-r*cos(theta)) term should be (r*cos(theta)).

Here we use the identity cos^2(theta)+sin^2(theta)=1.

The above result is another way of deriving the result dA=rdrd(theta).

Now we compute compute the Jacobian for the change of variables from Cartesian coordinates to spherical coordinates.

Recall that

The Jacobian is given by:

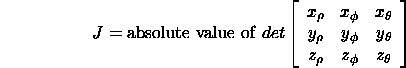
Plugging in the various derivatives, we get

Correction The entry -rho*cos(phi) in the bottom row of the above matrix SHOULD BE -rho*sin(phi). Computing this determinant, we get

[Vector Calculus Home] [Math 254 Home] [Math 255 Home] [Notation] [References]

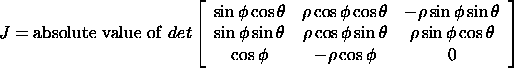
Copyright © 1996 Department of Mathematics, Oregon State University

If you have questions or comments, don't hestitate to contact us.