ANNOUNCEMENTS
MTH 437/537 — Spring 2024

6/15/24
The exams have been graded, and course grades assigned, although you may not be able to see them until tomorrow.
If you have any questions about how your final was graded or about your course grade, please contact me.
Answers to questions not asking you to show something are below.
  1. (b) $\frac{3m\pm\sqrt{9m^2-8q^2}}{2}$
  2. (a) $2\pi A$, $2B$
  3. $f(\rho)=\frac{m-\rho}{m+\rho}$, $h(\rho)=\frac{(m+\rho)^2}{2\rho^2}$ (constants may be different)
IF your grade were determined only by your final exam, it would be (out of 70; extra credit included):
6/11/24
Today's office hours via Zoom are confirmed for 1:30–3:30 PM.
Other times may be possible, and of course feel free to ask me questions via email.
6/10/24
My office hours today via Zoom are confirmed for 1:30–3:30 PM.
As noted below, the Zoom link is available as a Canvas announcement.
Please be patient if you are not admitted immediately.
Kieran Edward Dray was born Saturday evening.
Mother and baby (and the rest of us) are doing fine.
6/9/24
In problem 2, you may assume that the cosmological constant vanishes, that is, that $\Lambda=0$.
Please also remember that there are known errors in some of the results in the appendix of the textbook; see the errata page.
6/6/24
The Sage notebook I demonstrated in class for the Kerr metric can be found here.
This version uses an orthonormal frame but Sage takes much longer to compute the Riemann tensor using this method (quite possibly due to inefficient programming on my part). A version that uses the definition of the Kerr geometry that is built in to Sage using a coordinate basis can be found here,
I will hold office hours via Zoom on Monday (6/10) and Tuesday (6/11) at times to be announced, but most likely 1:30–3:30 PM.
The Zoom link has been posted as a Canvas announcement (and is the same as the link we used last term).
Other times are possible; ask! I will also respond as quickly as possible to questions sent via email.
6/5/24
The take-home final will be distributed online on Friday morning, 6/7/24, at 8 AM.
It will be due on Gradescope 48 hours from when you download it, but no later than midnight on Wednesday, 6/12/24.
With apologies, it appears that I never posted the curve on the midterm.
IF your grade were determined only by your adjusted midterm score (rounded to the nearest integer if necessary), it would be:
6/4/24
With apologies for the last-minute confirmation, class will meet as usual today.
(I was excused from jury duty.)
6/1/24
When using online resources to determine the Einstein tensor, be sure you know whether the calculation is being done in an orthonormal basis, or, more likely, in a coordinate basis. Although the computational methods are quite different in these two cases, it is straightforward to compare the answers obtained:
Tensor components always transform with the appropriate change of basis matrix; that's what makes them tensors.
This transformation is especially simple in orthogonal coordinates, where $\sigma^i = h^i dx^i$ (no sum) for some functions $h^i$.
For example, the statement that the Einstein tensor for the Robertson–Walker geometry has a component $G_{rr} = -\left( \frac{2a\ddot{a}+\dot{a}^2+k}{1-kr^2} \right)$ in a coordinate basis really means that the (symmetric, rank-2, covariant) tensor $G$ has the form $$G = ... - \left( \frac{2a\ddot{a}+\dot{a}^2+k}{1-kr^2} \right) dr\otimes dr + ...$$ (where we often omit "$\otimes$", as when writing the line element). Since we know that $\sigma^r=\frac{a}{\sqrt{1-kr^2}}\,dr$, we can rewrite this expression as $$G = ... - \left( \frac{2a\ddot{a}+\dot{a}^2+k}{a^2} \right) \sigma^r\otimes\sigma^r + ...$$ from which it is clear that $G_{rr} = -\left( \frac{2a\ddot{a}+\dot{a}^2+k}{a^2} \right)$ in an orthonormal basis (which some authors write as $G_{\hat{r}\hat{r}}$).
Both of these expressions can be written as $G_{rr}=-\left( \frac{2a\ddot{a}+\dot{a}^2+k}{a^2} \right) g_{rr}$, so long as $g_{rr}$ is expressed in the appropriate basis.
Since the components of $d\rr$ are the identity matrix in any basis, that is, since $g^i{}_j=\delta^i{}_j$, tensor components are easiest to compare when they have this "one up, one down" index structure, that is, as vector-valued 1-forms.
Sage code that computes the curvature for the Robertson–Walker geometry can be found here.
5/30/24
A discussion of Birkhoff's Theorem can be found in the Appendix.
The Sage code I demonstrated in class today can be found here.
5/28/24
As announced in class today, you may use computer algebra to perform the computations needed on HW #7.
As usual, you must document doing so, by attaching a printout of your session and explaining at least briefly what the computations mean.
As also announced in class today, the final exam will be a take-home exam. My current plan is outlined below; please let me know as soon as possible if you have any concerns about these arrangements.
5/25/24
All indices can be raised and lowered with the metric.
For example, since $\TT=T^i{}_j\sigma^j\ee_i$, we have $\ee_k\cdot\TT = T^i{}_j\sigma^j\ee_k\cdot\ee_i = g_{ki}T^i{}_j\sigma^j = T_{kj}\sigma^j$ and similarly for $\RR$ and $\GG$.
5/24/24
Several examples have been posted using Sage, including:
Further details about geodesic deviation can be found in §7 and §A.2 of the text, both of which can also be found here.
There are minor typos in the Schwarzschild curvature 2-forms as given in §A.3 of the text:
The coordinate expressions in the middle of Equations (A.52) and (A.53) are each missing a factor of 1/2.
Also, the initial minus sign should be removed from Equation (A.61).
However, the final expressions in terms of an orthonormal frame are correct.
The wiki version has been corrected, and a full list of errata can be found here.)
5/22/24
Here are my expectations for HW #6, due tomorrow:
5/21/24
A corrected version of the SageMath computation of the curvature of Schwarzschild geometry in rain coordinates shown in class today can be found here.
This version also substitutes $r=r(R,T)$ back in at the end. Compare the result with the computation in Schwarzschild coordinates also shown in class today, which can be found here.
5/16/24
There are several computer algebra packages available for computing curvature components:
Printouts of (old!) sample computer algebra sessions are available for GRTensor and CLASSI.
Older versions of my instructions, that also include coordinate-based computations, are available for Maple and Mathematica packages, and for SHEEP/CLASSI.
You may use software to compute curvature on the homework! See me if you would like help getting started.
You must however document doing so, and it's up to you to ensure that you are working in an appropriate basis.
5/15/24
Answers to the midterm questions are below. Solutions will be discussed briefly tomorrow in class, and can also be seen in my office.
  1. (a) $24\pi m$ (b) $12\sqrt3\pi m$
  2. (a) No (b) $1/\rho$ (c) $\boldsymbol{\hat\alpha}$ (d) $-1$ (e) $1/\rho^2$
  3. (a) $\rho\,\boldsymbol{\hat\alpha}$ (b) $\rho^2\dot\alpha$ (c) Many answers possible, including $\rho=e^{\pm\alpha}$
  4. (a) $r=m\pm\sqrt{m^2-q^2}$ (b) $-\sqrt{\frac{2m}{r}-\frac{q^2}{r^2}}$ (c) No
5/14/24
Further information about charged and rotating black holes and their Penrose diagrams can be found in the undergraduate textbook by d'Inverno, which is available in the OSU library.
A more advanced treatment can be found in the book The Large Scale Structure of Space-Time by Hawking & Ellis, which is also available in the OSU library.
5/12/24
During Thursday's review, I remarked that the Gaussian curvature needed for HW #5 can be computed as usual either extrinsically (use your embedding in $\EE^3$) or intrinsically (use the structure equations).
As noted by one student, there is a third method: Since the surface of revolution is isometric to the ($r,\phi$)-plane of the Schwarzschild geometry, you can use the Schwarzschild curvature 2-forms given in the text!
Yes, these curvature 2-forms, given in Appendix A.3 of DFGGR, are for the full, 4-dimensional Schwarzschild geometry. But a major advantage of working with differential forms is that you can always "use what you know" in order to restrict given results to subspaces. Here, it is enough to note $\Omega^\phi{}_r$ from (A.55). (Be careful with the signs, although it is not actually necessary to work out $\Omega^r{}_\phi$ using (A.57), since the Gaussian curvature is independent of orientation.)
5/11/24
My review notes can be found here.
A list of topics suggested by previous students can be found here.
I will hold extra office hours on Monday, 5/13.
I should be in my office from 11 AM–2 PM, although I will take a lunch break at some point.
5/9/24
As announced in class today, the midterm will not contain any questions about curvature.
Questions involving geodesics could involve determining the connection, but can likely be answered using the symmetry techniques discussed in class and reviewed today.
5/8/24
As mentioned in class last week, there are 10 independent Killing vectors in 4-dimensional Minkowsk space, namely 4 translations: $\xhat$, $\yhat$, $\zhat$, $\Hat{t}$; 3 rotations: $r\,\phat=x\,\yhat-y\,\xhat$, $y\,\zhat-z\,\yhat$, $z\,\xhat-x\,\zhat$; and 3 boosts: $x\,\Hat{t}+t\,\xhat$, $y\,\Hat{t}+t\,\yhat$, $z\,\Hat{t}+t\,\zhat$.
Each of these Killing vectors can be realized as coordinate symmetries of the line element in appropriate coordinates, e.g. by switching to round (spherical or cylindrical) or Rindler-like coordinates.
It is straightforward to show that each of the above vectors satisfies Killing's equation, namely $d\XX\cdot d\rr=0$. Less obvious (but not difficult to show) is that these are the only independent solutions of that equation.
The collection of all Killing vectors forms a Lie algebra under the operation of commutation, where vector fields act on each other by differentiation. Lie algebras are infinitesimal versions of Lie groups, representing continuous symmetries. For (some) further information, see Chapter 10 of our octonions book.
5/7/24
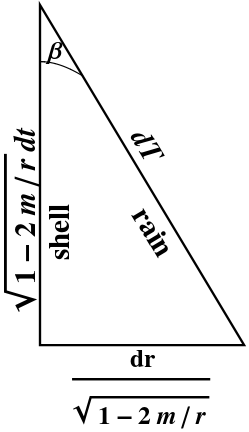Figure 3.9 on page 38 (also available as Figure 8 in this section), showing the relationship between shell coordinates and rain coordinates, is correct but misleading.
This figure shows the relationships between certain differential forms, using the geometric description of §13.8, but without displaying the stacks. However, it is not easy in such diagrams to read off the magnitudes of the differential forms, which do not correspond directly to the lengths of the sides.
A more traditional figure, using the language of infinitesimal displacement, is shown at the right.
Spacetime diagrams implicitly show relationships between vectors. For example, the figure at the right shows that $$d\rr = \sqrt{1-\frac{2m}{r}}\,dt\,\Hat{t} + \frac{dr\,\Hat{r}}{\sqrt{1-\frac{2m}{r}}} = dT\,\Hat{T}$$ if $dR=0$, that is, for a freely-falling object. Figure 3.9 shows instead a relationship between 1-forms, namely that $$1\,\sigma^T = \frac{\sigma^t}{\sqrt{1-\frac{2m}{r}}} + \frac{\sqrt{\frac{2m}{r}}\,\sigma^r}{\sqrt{1-\frac{2m}{r}}}$$ which is always true. (The explicit inclusion of orthonormal basis 1-forms restores the proper scaling to the triangle.)
5/6/24
With apologies, I neglected to update the course website over the weekend.
There is an assignment this week, which is hopefully reasonably straightforward.
Please let me know if this short timeline is an issue for you.
The formula sheet for the midterm has been posted.
5/2/24
There are two competing usages of "rain coordinates", due to the confusion between the two radial coordinates.
(The basis 1-forms $\sigma^T=dT$, $\sigma^R$ in rain coordinates are defined in §3.9, but the rain cooordinate $R$ is not defined until §A.4).
So "rain coordinates" should really refer to $(T,R,\theta,\phi)$, but is usually used as a synonym for Painlevé–Gullstrand coordinates.
Only the latterformer alternative corresponds to an orthogonal coordinate system, with line element $$ds^2 = -dT^2 + \frac{2m}{r}\,dR^2 + r^2 (d\theta^2+\sin^2\theta\,d\phi^2)$$ where $r$ is now an implicit function of $T$ and $R$.
Another way to see that surfaces with $\{T=\hbox{const}\}$ are flat is to note that $\sigma^R-\sqrt{\frac{2m}{r}}\,\sigma^T=dr$, so that $\sigma^R=dr$ if $dT=0$.
However, as pointed out in class, the $T$ and $R$ directions are orthogonal, but not the $T$ and $r$ directions.
Thus, the operator "$\frac{\partial}{\partial T}$" is ambiguous! Holding $R$ fixed, the resulting "$T$ direction" is not a symmetry, since the line element above depends on $T$ (through $r$). Holding $r$ fixed instead does lead to a symmetry; the Painlevé–Gullstrand line element has no $T$ dependence. However, the resulting "$T$ direction" is orthogonal to $r$, not $R$ — and is hence the same as the Schwarzschild $t$ direction, which we already know is a symmetry.
4/30/24
The midterm will be Tuesday, 5/14/24 (Week 7).
The main topics to be covered on the midterm are:
Further information:
4/23/24
The due date for the assignment due today at 4 PM (HW #3) has been extended until 4 PM on Thursday, 4/25/24.
You may resubmit your assignment without penalty until then.
(Assignments will not be accepted after the extended due date.)
4/21/24
When working on this week's assignment (HW #3), the discussion of circular orbits in §3.6 of DFGGR may be helpful.
As discussed both in class and in this section, we argued that $\dot r=0$ implies that $V'=0$.
4/19/24
The figures shown at the end of class yesterday can be found in §3.5 of the text.
Here are some hints for this week's assignment:
4/18/24
Further information about the difference between the geometric radius and the physical radius can be found in my recent paper on embedding diagrams, which was published here.
A construction of the Schwarzschild embedding diagram is included, which should be accessible to students in this class.
4/15/24
From the tagline of today's xkcd comic strip:
The standard North American NAD83 coordinate system is misaligned from the actual Earth, off-center by about 7 feet.
4/11/24
We didn't quite get to the derivation of the geodesic equation on the sphere...
The answer can be found in §19.3.
Solutions of the geodesic equation in polar and spherical coordinates can be found in §19.5 and §19.6.
The latter section also discusses using vector analysis to describe arbitrary geodesics on the sphere.
You should check for yourself that $r\phat$ is indeed a Killing vector, that is, that $d(r\phat)\cdot d\rr=0$ (in polar coordinates).
Details can be found in §2.2.
4/9/24
One important theme in yesterday's derivation of the geodesic equation is that differentials are the numerators of derivatives. Thus, an equation involving 1-forms can be converted to one involving derivatives by dividing by a differential.
A more subtle message is that this doesn't work for second derivatives. In particular, the geodesic equation is a second order system of ODEs, but there is no way to take two derivatives with respect to the same parameter using differential forms...
4/8/24
I will be speaking about the mathematical side of my current research next Monday in the Geometry and Topology Seminar.
Octonions and the exceptional Lie algebras (and particle physics)
Tevian Dray
M 4/15/24 at 12 PM in Kidder 280
4/5/24
As pointed out in class yesterday, the sets of spacelike, timelike, and lightlike vectors do not close under addition (even with the zero vector included), and thus do not form a vector space. (Can you find counterexamples?)
However, the set of future-pointing (or past-pointing) timelike vectors do close under addition (with the zero vector included). and therefore do form a vector space. [Still not a vector space since additive inverses are missing.]
As discussed in class yesterday, the resolution of the twin paradox is that only one of the twins is in an inertial frame. But what if the spatial topology were closed, that is, what if the universe looked like a cylinder, with $x=0$ identified with $x=\lambda$? Then the traveling twin doesn't need to accelerate...
Try to resolve this version of the paradox yourself before looking up the answer; a complete discussion can be found here.
4/4/24
A recording of a talk I gave a couple of years on the geometry of special relativity, covering essentially the same content as we did in class this week, can be found here.
There is also a poster describing my geometric approach to special relativity near Weniger 304.
The slides I showed in class today can be found here.
Several of these slides also appear in the video.
A few people haven't yet completed HW #0, which was due today.
There are no formal penalties for skipping this assignment, but submission would still be appreciated.
The optional meeting to go over the final from last term will indeed start at 10:30 AM next Tuesday, 4/9/24, in Weniger 328.
If you can't make it to this meeting, please feel free to ask about the exam during office hours.
4/2/24
As announced in class today, I will schedule an optional meeting to discuss the final exam from last term. We tentatively agreed that this meeting would be sometime on Tuesday morning, 4/9/24. I propose starting at 10:30 AM, but am willing to consider earlier times.
Please let me know if you would like to attend and this time will not work for you.
4/1/24
A schedule from a previous year can be found here.
This schedule is a good approximation to what we will cover when.
3/26/24
All assignments will be posted only on the homework page.
Assignments will not be posted on Canvas.
All assignments should be submitted via Gradescope.
Further information can be found on my own information page for Gradescope.
3/25/24
The primary text for this course will be my own book, which can be read online as an ebook through the OSU library.
There is also a freely accessible wiki version available, which is however not quite the same as the published version.
We will also refer briefly to my book on special relativity.
You may purchase this book if you wish, but it can also be read online as an ebook through the OSU library, and again there is also a wiki version.
You may also wish to purchase a more traditional text, in which case I recommend any of the first three optional texts listed on the books page. The level of this course will be somewhere between that of these books, henceforth referred to as EBH (Taylor & Wheeler), Relativity (d'Inverno), and Gravity (Hartle).
We will cover more material than EBH, but we will stop short of the full tensor treatment in Relativity or (the back of) Gravity. We will also cover some of the material on black holes from EBH which is not in Gravity or Relativity.
In short, none of these books is perfect, but all are valuable resources. In addition to the above books, OSU owns an electronic copy of Relativity Demystified, which summarizes many of the key aspects of relativity, but provides no derivations. By all means use it for reference, but I would not recommend using it as a primary text.