MTH 655 - Sec 010

(Cross-listed with MTH659 for those who have previously taken a different MTH655)

Numerical Analysis:
Uncertainty Quantification

MWF 9:00-9:50 AM
MFD112
Winter 2023


Professor:

Dr. Nathan Louis Gibson  

Office:

Kidd 056

Office Hours:

Monday and Friday 10AM; Wednesday 11AM

Course Website: 

https://sites.science.oregonstate.edu/~gibsonn/Teaching/MTH655-010W23

 

Course Description

Background:

Accurate estimates for the propagation of uncertainty through complex systems is necessary for predictive simulation, robust design, and failure analysis. This course is primarily concerned with the numerical solution of differential equations which include uncertainty, either in system parameters, source terms, or in initial/boundary conditions.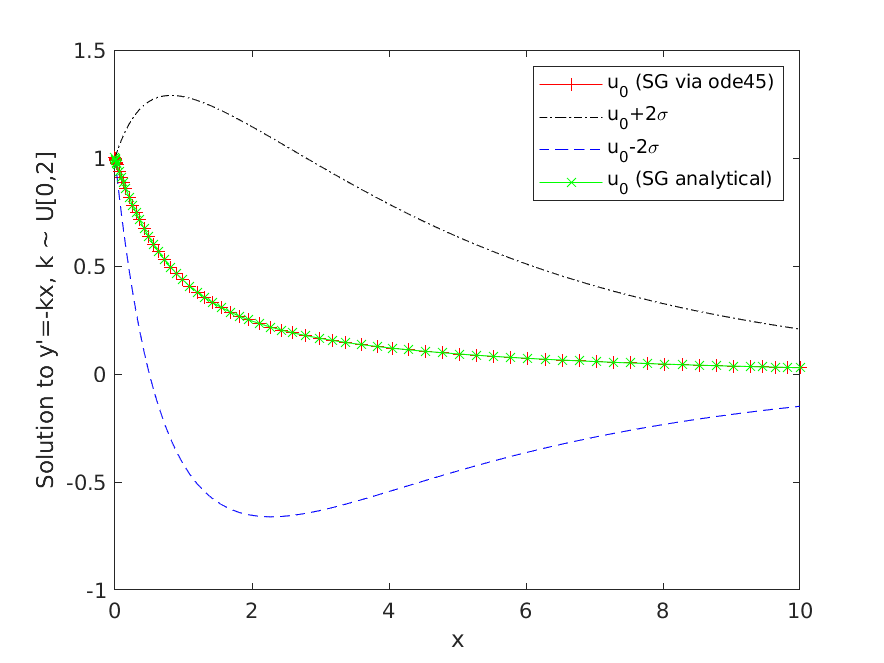		 

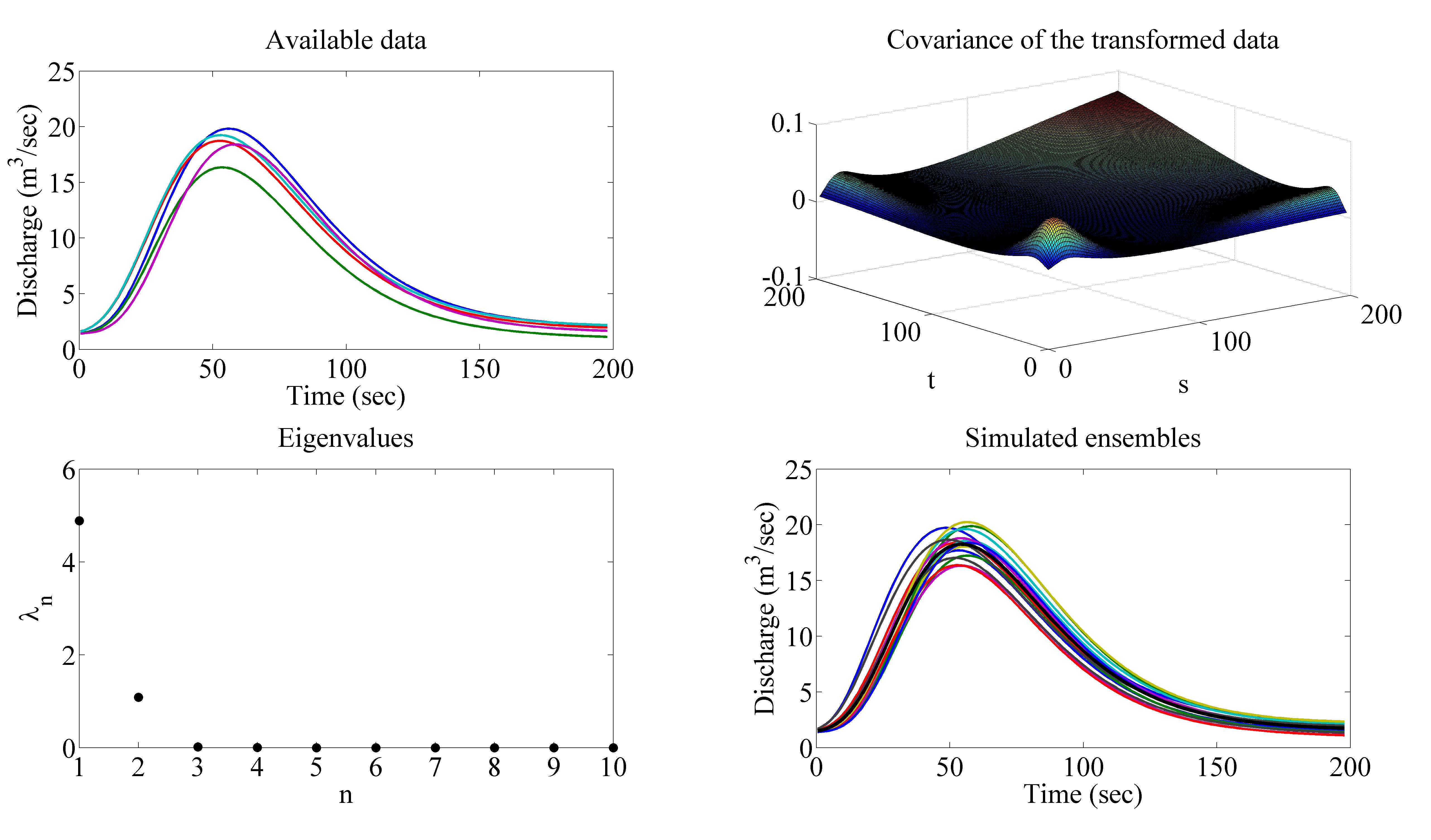
Fig: Stochastic Galerkin approximation for a Random ODE

Content:

In this course we will develop basic mathematical foundations and algorithmic aspects of stochastic computations and uncertainty quantification theory. The necessary background in polynomial approximation, numerical integration, and probability theory will be developed. While the emphasis will be on random differential equations, stochastic differential equations will also be discussed. Methods covered will include Karhunen–Loève expansion, Stochastic Galerkin including generalized Polynomial Chaos, Stochastic Collocation including Smolyak sparse grids, Spectral Stochastic Finite Element Method, Euler-Maruyama method for SDEs, among others. Topics will include convergence, stability, error estimates and implementation issues. As time allows, we will discuss challenges arising from high-dimensional problems, inverse problems/robust optimization and data assimilation. The course will provide a working understanding of several numerical solution methods as well as MATLAB sample codes for examples of applications.


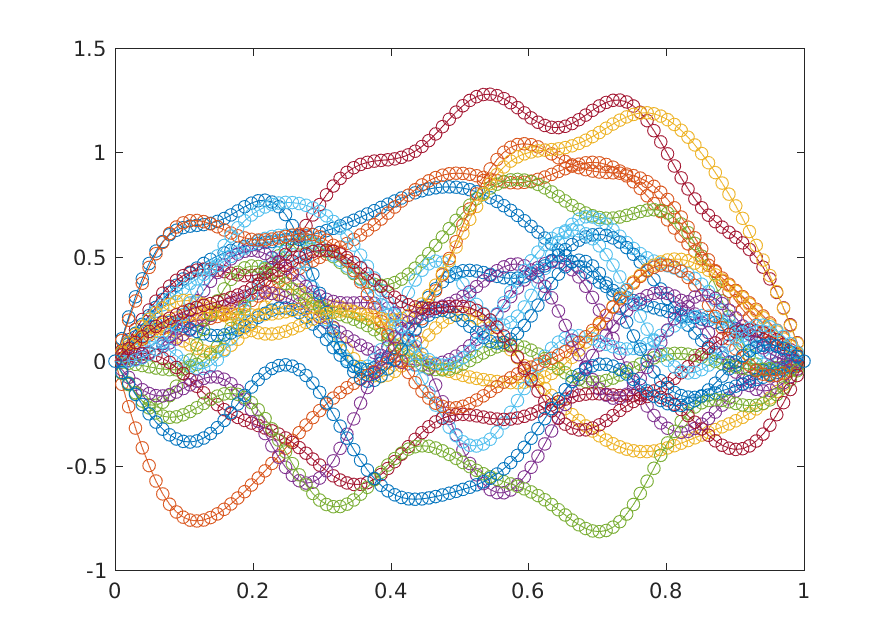
Fig: Karhunen–Loève expansion approximation to a Brownian Bridge

Learning Outcomes:

The course is intended for graduate students of mathematics, computer science, statistics, and other science and engineering disciplines. The content of the course is largely self-contained. For general pre-requisites, students should have some familiarity with probability, linear algebra, ordinary and partial differential equations, and introductory numerical analysis. Please contact the instructor with questions about background.

Measurable Student Learning Outcomes: A successful student in MTH 656/659 will be able to:

  • Model sources of uncertainty for a particular problem
  • Identify the appropriate method for uncertainty quatification in a given application
  • Apply standard uncertainty quantification techniques to systems such as random ODEs and stochastic ODEs
  • Assess convergence rates of schemes
  • Analyze stability and accuracy properties of schmes
  • Synthesize fully discrete schemes by incorporating temporal, spatial and stochastic discretizations
  • Evaluate trade-offs of accuracy and efficiency of methods

Text:

There is no required text for the course, but the following are recommended (in order of importance):
  1. Dongbin Xiu. Numerical methods for stochastic computations: a spectral method approach. Princeton University Press, 2010.
  2. Ralph C Smith. Uncertainty Quantification: Theory, Implementation, and Applications, volume 12. SIAM, 2013.
  3. Desmond J. Higham, An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations, SIAM Review, vol 43, No 3, pp 525-546, 2001.
  4. T.J. Sullivan. Introduction to Uncertainty Quantification, Springer, 2015.
  5. Kloeden and Platen. Numerical Solution of Stochastic Differential Equations, Springer, 1999.
  6. Roger G Ghanem and Pol D Spanos. Stochastic Finite Elements: A Spectral Approach. Courier Dover Publications, 2003.
  7. Olivier P Le Maitre and Omar M Knio. Spectral methods for uncertainty quantification: with applications to computational fluid dynamics. Springer, 2010.

Grades

Course requirements will be homework assignments, which will consist of a mixture of analytical work and numerical computations with MATLAB, as well as a term project on a topic chosen by the student.

Grade Distribution:

Homework 50%
Final Project50%
Total 100%

Homework

Homework is required for this course. There will be a few short assignments, and they will be posted on the website. Problems will reinforce theoretical and computational concepts from lecture. Students are encouraged to work together, but must turn in individual papers.

Term Project

A computational/mathematical project is required for this course. Students must work individually on a topic/problem of their choice involving random or stochastic problems (can be from research/thesis work). Students must submit a typed (less than or equal to two pages) research proposal, including questions to be answered midway through the course. Final papers will be submitted as a typed report, including tables or graphs as figures with captions and references to these inside the body of the text, and a bibliography with at least two external sources. Each student will give brief (10 minute) presentation on their results during the last day of classes or the day reserved for a final exam.

Matlab

Matlab codes will be provided for homework assigments.

Oregon State University has subscribed to a Total Academic Headcount (TAH) Site License for MATLAB. This new licensing includes many, but not all MATLAB toolboxes. OSU faculty, staff and students can install on up to 4 personally-owned devices or computers. For more information visit Information Services -- MATLAB or matlab.mathworks.com.

The following are online resources for learning Matlab:

Supplements

Presentations:
Uncertainty Quantification Methods with Applications
Gradient-based Methods for Optimization: Part 1 & Part 2
Electromagnetic Relaxation Time Distribution Inverse Problems in the Time-domain
Finite Difference, Finite Element and Finite Volume Methods for the Numerical Solution of PDEs
Polynomial Chaos Approach for Maxwell's Equations in Dispersive Media
Stochastic Spectral Approaches to Bayesian Inference
Uncertainty Quantification Methods for Multiscale Modeling and Dimension Reduction

Samples:
Comparision of Stochastic Galerkin and Stochastic Collocation for a simple example scalar linear ODE
Files for creating plots in Optimization presentation
Sample Beamer Presentation
Sample Latex Report

References:
McKenzie Masters Paper
B Johnson, NL Gibson, E Cotilla-Sanchez, A Coupled Karhunen-Loeve and Anisotropic Sparse Grid Interpolation Method for the Probabilistic Load Flow Problem Electric Power Systems Research, Volume 193, April 2021.
Duan Chen, Arturo S Leon, Nathan L Gibson, Parnian Hosseini, "Dimension reduction of decision variables for multireservoir operation: A spectral optimization model", Water Resources Research, 52 (1), 2016.
NL Gibson, "A Polynomial Chaos Method for Dispersive Electromagnetics", Communications in Computational Physics, vol. 18, issue 5, pp 1234-1263, 2015. (pre-print).

Intro to Data Assimilation
Intro to Kalman Filter
Kalman Filter via Linear Algebra
Convergence of Stochastic Collocation Burkardt Software Repository