- §1. Step Functions
- §2. The Dirac Delta Function
- §3. Exercise: Delta Functions 1
- §4. Properties of the Dirac Delta Function
- §5. Exercise: Delta Functions 2
- §6. Representations of the Dirac Delta Function
- §7. The Dirac Delta Function in Three Dimensions
- §8. The Dirac Delta Function and Densities
- §9. Exponential Representation of the Dirac Delta Function and Densities
Step Functions
The step function $\Theta(x)$, also called the Heaviside
function or theta function, is defined to be $0$ if $x<0$ and $1$ if $x>0$. See Figure 1. 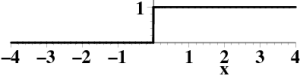 Figure 1: The step function $\Theta(x)$.
Figure 1: The step function $\Theta(x)$.
Step functions are used to model idealized physical situations where some quantity changes rapidly from one value to another in such a way that the exact details of the change are irrelevant for the solution of the problem, e.g. edges of materials or a process that switches on abruptly at a particular time, etc.
By shifting the argument of the function, it is possible to put the discontinuity of the theta function wherever we need it. In Figure 2 you can see that the graph of $\Theta(x-2)$ has discontinuity at $x=2$, instead of at $x=0$. 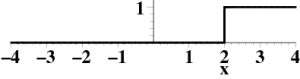 Figure 2: The function $\Theta (x-2)$.
Figure 2: The function $\Theta (x-2)$.
The the step function can also be used to turn a function off, since \begin{equation} \Theta(-x) = 1-\Theta(x) \end{equation} is a step down, rather than up.
Make sure that you are able to graph all of the following functions: \begin{eqnarray*} f(x) &=& 2\Theta(x)\\ f(x) &=& \Theta(x-2)\\ f(x) &=& \Theta(2x-3)\\ f(x) &=& \Theta(2-x)\\ f(x) &=& \Theta(x)\>\Theta(x-2)\\ f(x) &=& \Theta(x)-\Theta(x-2)\\ f(x) &=& \sin x\>\Theta(x-\frac{\pi}{2}) \end{eqnarray*}
In most physical problems, it is unnecessary to know the exact value of $\Theta(x)$ at the discontinuity. If it ever matters, it is usually easiest to define it symmetrically, i.e. \begin{equation} \Theta(0) = \frac12 \end{equation}