You are here: start » book » linalg » deltaintro
- §1. Step Functions
- §2. The Dirac Delta Function
- §3. Exercise: Delta Functions 1
- §4. Properties of the Dirac Delta Function
- §5. Exercise: Delta Functions 2
- §6. Representations of the Dirac Delta Function
- §7. The Dirac Delta Function in Three Dimensions
- §8. The Dirac Delta Function and Densities
- §9. Exponential Representation of the Dirac Delta Function and Densities
The Dirac Delta Function
The Dirac delta function $\delta(x)$ is not really a “function”. It is a mathematical entity called a distribution which is well defined only when it appears under an integral sign. It has the following defining properties: \begin{equation} \delta(x) = \cases{0, \qquad &if $x\not= 0$\cr \infty, \qquad &if $x=0$\cr} \end{equation} \begin{equation} \int_b^c \delta(x)\, dx = 1 \qquad\qquad b<0<c \end{equation} \begin{equation} x\,\delta(x) \equiv 0 \end{equation}
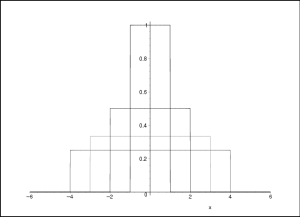
It may be easiest to think of the delta function as the limit of a sequence of steps, each of which is higher and narrower than the previous step, such that the area under the step is always one; see Figure 1.
The properties of the delta function allow us to compute \begin{eqnarray} \Int_{-\infty}^{\infty} f(x)\,\delta(x) \,dx &=& \Int_{-\infty}^{\infty} f(0)\,\delta(x) \,dx \\ &=& f(0) \Int_{-\infty}^{\infty} \delta(x) \,dx \nonumber\\ &=& f(0) \nonumber \end{eqnarray} We can shift the “spike” in the delta function as usual, obtaining $\delta(x-a)$. This shifted delta function satisfies \begin{equation} \Int_{-\infty}^{\infty} f(x)\,\delta(x-a) \,dx = f(a) \end{equation} Thus, the Dirac delta function can be used to pick out the value of a function at any desired point.
We can relate the delta function to the step function in the following way. Consider the function $g(x)$ given by the integral \begin{equation} g(x)=\Int_{-\infty}^x \delta(u-a)\,du \end{equation} Notice the variable $x$ in the upper limit of the integral. The value of this function $g(x)$ is $0$ if we stop integrating before we reach the peak of the delta function, i.e. for $x<a$. If we integrate through the peak, the value of the integral is $1$, i.e. for $x>a$. Thus, we have argued that the value of the integral, thought of as a function of $x$, is just the step function \begin{equation} \Theta(x-a) = \Int_{-\infty}^x \delta(u-a)\,du \end{equation} (Recall that we don't really care about the choice of $\Theta(0)$, so we don't need to worry about the value of this function if we stop integrating exactly at $x=a$.)
If the step function is the integral of the delta function, then the delta function must be the derivative of the step function. \begin{equation} \frac{d}{dx}\Theta(x-a) = \delta(x-a) \label{fdelta} \end{equation} You should be able to persuade yourself that this statement is reasonable geometrically if you think of the derivative of a function as representing its slope.