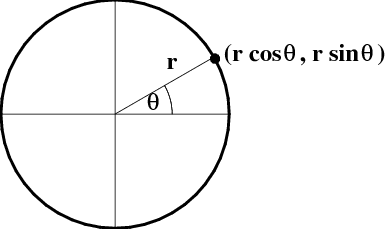Figure 3.2: Defining the (circular) trigonometric functions via a circle.

Consider a point $P$ on the circle of radius $r$, as shown in Figure 3.2. The angle $\theta$ between the line from the origin to $P$ and the (positive) $x$-axis is defined as the ratio of the length the arc of a circle between $P$ and the point $(r,0)$ to the radius $r$. 1) Denoting the coordinates of $P$ by $(x,y)$, the basic (circular) trig functions are then defined by \begin{eqnarray} \cos\theta &=& \frac{x}{r} \label{cosdef}\\ \end{eqnarray}\begin{eqnarray} \sin\theta &=& \frac{y}{r} \label{sindef}\\ \end{eqnarray}\begin{eqnarray} \tan\theta &=& \frac{\sin\theta}{\cos\theta} \end{eqnarray} and the fundamental identity \begin{equation} \cos^2\theta + \sin^2\theta = 1 \end{equation} follows from the definition of a circle. We have the well-known addition formulas 2) \begin{eqnarray} \sin(\theta+\phi) &=& \sin\theta\cos\phi + \cos\theta\sin\phi \label{sinadd}\\ \end{eqnarray}\begin{eqnarray} \cos(\theta+\phi) &=& \cos\theta\cos\phi - \sin\theta\sin\phi \label{cosadd}\\ \end{eqnarray}\begin{eqnarray} \tan(\theta+\phi) &=& {\tan\theta+\tan\phi \over 1-\tan\theta\tan\phi} \label{tan} \end{eqnarray} as well as the derivative formulas 3) \begin{eqnarray} {d\over d\theta} \sin\theta &=& \cos\theta \\ {d\over d\theta} \cos\theta &=& -\sin\theta \end{eqnarray}