The key concept in Euclidean geometry is the distance function that measures the distance between two points. In two dimensions, the (squared!) distance between a point $B=(x,y)$ and the origin is given by \begin{equation} r^2 = x^2 + y^2 \end{equation} which is of course just the Pythagorean Theorem; see Figure 3.1.

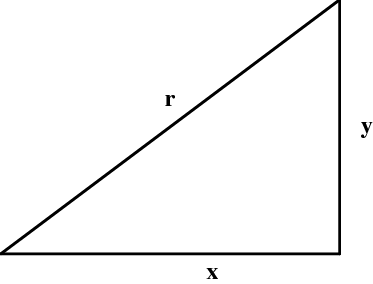Figure 3.1: Measuring distance in Euclidean geometry using the Pythagorean Theorem.

It is natural to study the set of points that are a constant distance from a given point, which of course form a circle.