We now return to the question of how “wide” things are.

Consider first a meter stick at rest. In spacetime, the stick “moves” vertically, that is, it ages. This situation is shown in the first sketch in Figure 6.2, where the horizontal lines show the meter stick at various times (according to an observer at rest). How “wide” is the worldsheet of the stick? The observer at rest of course measures the length of the stick by locating both ends at the same time, and measuring the distance between them. At $t=0$, this corresponds to the two heavy dots in the sketch, one at the origin and the other on the unit hyperbola. But all points on the unit hyperbola are at an interval of 1 meter from the origin. The observer at rest therefore concludes, unsurprisingly, that the meter stick is 1 meter long.

 
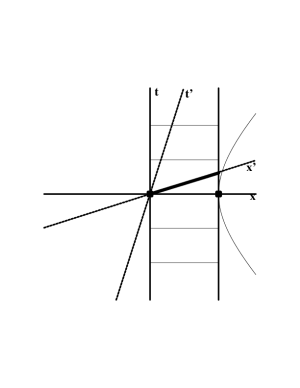
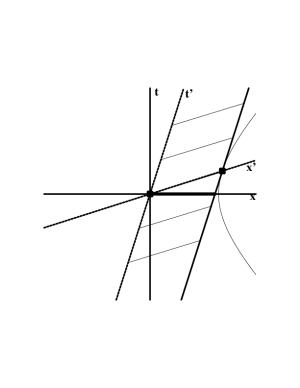
Figure 6.2: Length contraction as a hyperbolic projection.

How long does a moving observer think the stick is? This is just the “width” of the worldsheet as measured by the moving observer. This observer follows the same procedure, by locating both ends of the stick at the same time, and measuring the distance between them. But time now corresponds to $t'$, not $t$. At $t'=0$, this measurement corresponds to the heavy line in the first sketch in Figure 6.2, Since this line fails to reach the unit hyperbola, it is clear that the moving observer measures the length of a stationary meter stick to be less than 1 meter. This is length contraction.

To determine the exact value measured by the moving observer, it is only necessary to note that both triangles in Figure 6.2 are (hyperbolic) right triangles, with the heavy line indicating the hypotenuse in each case. Simple (hyperbolic) trigonometry shows immediately that the hypotenuse of a right triangle with angle $\beta$ and adjacent side of length 1 is given by $1/\cosh\beta$.

For those who prefer an algebraic derivation, compute the intersection of the line $x=1$ (the right-hand edge of the meter stick) with the line $t'=0$ (the $x'$-axis), or equivalently $\cc t = x \tanh\beta$, to find that \begin{equation} \cc t = \tanh\beta \end{equation} so that $x'$ is just the interval from this point to the origin, which is \begin{equation} x' = \sqrt{x^2 - \csq t^2} = \sqrt{1-\tanh^2\beta} = \frac{1}{\cosh\beta} \end{equation}

What if the stick is moving and the observer is at rest? This situation is shown in the second sketch in Figure 6.2. The worldsheet now corresponds to a “rotated rectangle”, indicated by the parallelograms in the sketch. The fact that the meter stick is 1 meter long in the moving frame is shown by the distance between the two heavy dots (along $t'=0$), and the measurement by the observer at rest is indicated by the heavy line (along $t=0$). Again, it is clear that the stick appears to have shrunk, since the heavy line fails to reach the unit hyperbola.

Thus, a moving object appears shorter by a factor $1/\cosh\beta$. It doesn't matter whether the stick is moving, or the observer; all that matters is their relative motion.