- §1. Distance
- §2. Trigonometry
- §3. Triangle Trig
- §4. Rotations
- §5. Projections
- §6. Addition Formulas
Triangle Trig
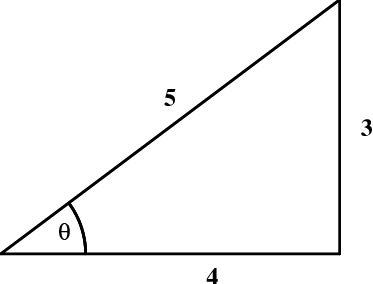 Figure 3.3: A triangle with $\tan\theta={3\over4}$.
Figure 3.3: A triangle with $\tan\theta={3\over4}$.
An important class of trigonometric problems involves determining, say, $\cos\theta$ if $\tan\theta$ is known. One can of course do this algebraically, using the identity \begin{equation} \cos^2\theta = {1\over1+\tan^2\theta} \end{equation} But it is often easier to do this geometrically, as illustrated with the following example.
Suppose you know $\tan\theta={3\over4}$, and you wish to determine $\cos\theta$. Draw any triangle containing an angle whose tangent is $3\over4$. In this case, the obvious choice would be the triangle shown in Figure 3.3, with sides of 3 and 4. What is $\cos\theta$? The hypotenuse clearly has length $5$, so that $\cos\theta={4\over5}$.
Trigonometry is not merely about ratios of sides, it is also about projections. Another common use of triangle trigonometry is to determine the sides of a triangle given the hypotenuse $r$ and one angle $\theta$. The answer, of course, is that the sides are $r\cos\theta$ and $r\sin\theta$, as shown in Figure 3.4.
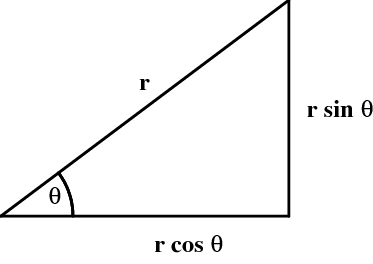 Figure 3.4: A triangle in which the hypotenuse and one angle are known.
Figure 3.4: A triangle in which the hypotenuse and one angle are known.