- §1. Non-Euclidean Geometry
- §2. The Hyperboloid
- §3. The Poincaré Disk
- §4. The Klein Disk
- §5. The Pseudosphere
The Klein Disk
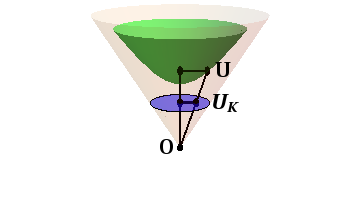 Figure 14.5: Constructing the Klein disk.
Figure 14.5: Constructing the Klein disk.
The Klein Disk model of hyperbolic geometry is also a projection of the hyperboloid. This time, however, we project from the origin into the plane $t=\sigma$. Thus, the point $U$, with coordinates given by (Equation (4) of §14.2), would be mapped to the point \begin{equation} U_K = (\sigma\,\tanh\beta\cos\phi,\sigma\,\tanh\beta\sin\phi,\sigma) \end{equation} as shown in Figure 14.5, The image of the hyperboloid is again the interior of a disk, this time the disk of radius $\sigma$ in the plane $t=\sigma$. The constant $\sigma$ can lie between $0$ and $\rho$, as shown in the figure, although it is useful to choose $\sigma=\rho$, in which case the disk is actually tangent to the hyperboloid at its tip.
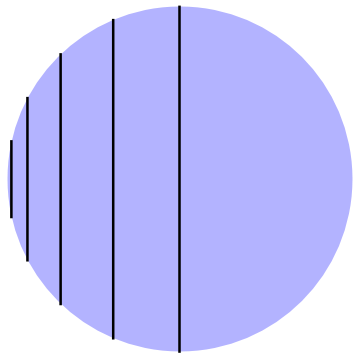
Since lines on the hyperboloid are contained in planes through the origin, and since planes intersect in straight (Euclidean) lines, the Klein Disk model has the nice feature that lines are Euclidean; the lines of the Klein Disk model are the chords of the circle bounding the disk, as shown in Figure 14.6. This feature is at first sight much nicer than any of the previous models, in which “lines” bear little resemblance to Euclidean lines. However, this simplicity comes at a price. More algebra reveals that the hyperboloid line element, rewritten using coordinates from the Klein Disk, takes the form \begin{equation} ds^2 = \frac{\rho^4\,dK^2}{(\rho^2-K^2)^2} + \frac{\rho^2\,K^2\,d\phi^2}{(\rho^2-K^2)} \end{equation} where \begin{equation} K = \rho\,\tanh\beta \end{equation} is the radial coordinate in the Klein Disk. Due to the different denominators in the two terms, the line element is no longer conformal to the Euclidean metric! This means that angles can not be measured with a Euclidean protractor in the Klein Disk model.