ANNOUNCEMENTS
MTH 254H — Fall 2015

12/10/15

The final has been graded, and course grades have been assigned. They should show up online tomorrow.

You can get your exam back if you stop by my office next term.
If you'd like to know your exam score before then, send me an email request using a campus address.

I have also made some minor corrections to the exam answers given below.

12/9/15

Below are the answers to the final. Full solutions can be seen in my office.

1. $2$

2. $4\pi$

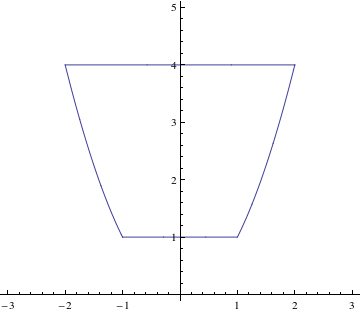
3. (a) $\int_0^{2\pi}\int_2^3 r^3\,dr\,d\phi$ (or $\int_0^{2\pi}\int_2^3\int_0^{r^2} r\,dz\,dr\,d\phi$) (b) see figure at right

4. saddle @ $(0,1)$ and $(2,-1)$; local max @ $(0,-1)$; local min @ $(2,1)$; $12$, $4$

5. $4$, $-4$

6. approximate answers: $-2\hat{x}+4\hat{y}$, $2\sqrt{5}$ (both in ${}^\circ\hbox{C/m}$)

7. (a) $\frac23\hat{x}+\frac13\hat{y}+\frac23\hat{z}$ (b) $3$ (c) $0$ (all in ${}^\circ\hbox{C/ft}$)

8. (a) $0$ ft/mi (b) $-7$ ft/mi (c) ${7}/{\sqrt2}$ ft/mi

9. (a) $4$ (b) $0$ (c) $\vec{0}$ (d) $2\hat{z}$ (e) $\frac\pi2$

10. (a) $\frac45\hat{x}+\frac35\hat{y}$ (b) straight line

EC. $\frac{81\pi}{5}$

12/4/15

As promised, here are some further resources for review.

• Suggested problems from Briggs/Cochran:
  • §11.1: 1–43;
  • §11.3: 13–18, 38–42;
  • §11.4: 7–28;
  • §11.6: 13–20;
  • §11.7: 7–14;
  • §12.6: 9–26 (and then perhaps 27–48);
  • §12.8: 9–28, 37–44, 54–57;
  • §12.9: 5–10 (and then perhaps 17–26, 38–43).
  (Only do as many of the problems in a given group as you feel you need — doing all of them is too many!)
• Pictures of the review on the side board can be found here, here, here, and here.
• Here are 3 different solution strategies for the constrained optimization problem discussed in class today (and given below, dated 11/23/15):
  1. Substitution:
     Solve the quadratic equation $x^2+xy+y^2=3$ for $y$, obtaining $y=\frac{-x\pm\sqrt{12-3x^2}}{2}$. Now substitute this result into $x^2+y^2$, differentiate with respect to $x$, set the result equal to $0$, and solve for $x$. The algebra is messy! You will eventually need to square both sides and factor, leading to $(x^2-3)(x^2-1)=0$. Now solve for $x$, use the expression above to determine $y$, and make a table.
  2. Lagrange multipliers (this is what we did in class):
     Eliminate $\lambda$ from $\nabla(x^2+y^2)=\lambda\nabla(x^2+xy+y^2)$, and solve for $y$ in terms of $x$, obtaining $y=\pm x$. Substitute the result into $x^2+xy+y^2=3$ to get the critical boundary points, and make a table.
  3. Differentials:
     Zap $x^2+xy+y^2=3$ with $d$ and solve for $dy$. Substitute the result into $d(x^2+y^2)$, set the result equal to zero, and solve for $y$ in terms of $x$, again obtaining $y=\pm x$. Now proceed as for Lagrange multipliers.
  Method 1 is too hard to be useful in this case, so you should be comfortable using at least one of Methods 2 and 3.
• We didn't have time for a directional derivative problem in class. Remember that directional derivatives take the form $\frac{df}{ds}$, where $s$ refers to distance in the desired direction. From the Master Formula, we have $\frac{df}{ds}=\nabla{f}\cdot\frac{d\vec{r}}{ds}=\nabla{f}\cdot\hat{T}$, since $ds=|d\vec{r}|$; $\hat{T}$ is the unit vector in the desired direction. (In practice, directional derivatives can be computed using the last expression, without needing $d\vec{r}$ or the Master Formula.)
• We did not cover arclength, although the basic idea is simple: $ds$ measures distance along any curve. So compute $ds^2=d\vec{r}\cdot d\vec{r}=dx^2+dy^2+dz^2$ using what you know about the curve, take the square root, and integrate along the curve to get its length. (No, this won't be on the exam.)

12/2/15

Regarding today's activity on Change of Variables:

• The correct answers are $\int_D dA = 27\ln2$ and $\int_D \frac{y}{x}\,dA = \frac{81}{2}$.
• You are strongly encouraged to work out one of the integrals without using change of variables.
• Pictures of the side board can be found here, here, and here.
• You are also strongly encouraged to work out the area of the parallelogram shown in the first example today, both using the cross product and using an ordinary double integral (again, without change of variables). The correct answer is $\frac{12}{5}$.
• Change of variables will not be a required part of the final.

There will be a MTH 254 review session by another instructor on Tuesday 12/8/15 from 2–4 PM, in TBA LInC 200.

You are welcome to participate fully in this review, but please give other students priority, both in terms of access to the room should it be crowded, and in asking questions.

12/1/15

Extra office hours:

Wednesday, 12/2/15: I will extend my scheduled office hour (1:30–2:30 PM) so long as there are questions.

Friday, 12/4/15: 11–11:45 AM and from 1:15 PM until there's nobody left.

Monday, 12/7/15: TBA, but probably 10:30–11:30 AM and 1:30–2:30 PM.

Other times may be possible; ask.

11/30/15

The final will be Tuesday 12/8/15 from 6:00–7:50 PM in Kear 305.

• The final will be somewhat less than twice as long as the midterm
• It will cover material from the entire course, but with an emphasis on material since the midterm.
• The main new topics (roughly 55–65% of the exam) are:
  • vectors & vector functions;
  • gradient;
  • optimization;
• The old material (roughly 35–45%) is described below in the midterm announcement.
• Together, these topics correspond roughly to §11, §12, & §13 in Briggs/Cochran.
• You may bring two 3″×5″ index cards (both sides) of handwritten notes, or the equivalent.
• Other rules are as announced below for the midterm.
• Friday's lecture will be devoted to review. Come prepared to ask questions!

11/23/15

Here is another constrained optimization problem to practice with:

Find the maximum and minimum values of $x^2+y^2$ on the ellipse $x^2+xy+y^2=3$.
(Answer: max: $6$; min: $2$)

11/18/15

The schedule has been updated to reflect the 2-day Thanksgiving holiday next week.

There will be class on Wednesday, 11/25. We will do an activity involving surfaces that will reinforce the rather challenging concept of Lagrange multipliers, to be introduced on Monday, followed by an introduction to the relatively easy concept of how to describe curves.

The algebra actually isn't that bad when solving today's box problem using differentials:

• Zap both equations with $d$.
• Solve $dV=0$ for $dz$.
• Plug the result into $dA$.
• After simplifying the algebra, you should now be left with $dA=(x-2z)\frac{y}{x}\,dx+(y-2z)\frac{x}{y}\,dy$.
• Setting (both coefficients in) $dA$ to $0$ now yields $x=y=2z$, from which the final answer follows.

11/16/15

Here's the example I suggested at the end of class today:

Find and classify the critical points of the function $p(x,y) = \frac12 x^2 + 3y^3 + 9y^2 -3xy + 9y -9x$.
(Answer: local min at $(12,1)$; saddle at $(3,-2)$.)

11/13/15

Strange but true: The 13th of the month is more likely to be a Friday than any other day of the week!

Give up? Further information is available here.

11/9/15

Further discussion of the hill activity can be found in this article (by a former MTH 255 TA who is now a math professor), as well as in this followup article.

11/6/15

With apologies, part (d) of this week's homework should have asked for a positive $\hat{z}$ component; as worded, the requirement is automatically satisfied (and there are 2 correct answers).

11/1/15

Two mathematicians are talking on the telephone. Both are in the continental United States. One is in a West Coast state, the other is in an East Coast state. They suddenly realize that the correct local time in both locations is the same! How is this possible?

Give up? Some hints can be found here.

10/31/15

Below are the answers to the midterm. Full solutions can be seen in my office.

1. (a) FALSE (b) TRUE (c) FALSE

2. $90$

3. $0$

4. $7\pi/3$

5. $16/3$

6. (a) $2y~$ (b) $3y\,\cos(3xy)~$ (c) $3\cos(3xy)-9xy\,\sin(3xy)~$ (d) $7(x^2+x-y)^6(2x+1)$

7. $y=(9-x)/4$

8. $-15/8$, $5$, $25/8\sqrt2$

EC. $2$

10/28/15

Here are some further resources that may be helpful while preparing for the midterm:

• Pictures of my approaches to the resistor problem can be found here, here, and here.
• A picture of my review summary can be found here.

Here are the two review problems I posed during class:

• Find the mass of a (spherical) golf ball of radius 3 cm if the density in grams per cubic centimeter at any point is a constant $k$ times the distance from the center in centimeters.    (Answer: $81\pi/5$)
• Evaluate $\int_0^3\int_y^3 3\,\sqrt{x^2+16} \>\>dx\,dy$.    (Answer: 61)

Here is a selection of problems from Briggs/Cochran that may help you review. Do only as many as you feel you need to.

• §12.4: 7–39; §12.5: 7–14 & 60
• §13.2: 9–34 & 43–50; §13.3: 19 & 23; §13.4: 25–34 (optional challenge: 35–38); §13.5: 15–22 & 30–31;

A good strategy when integrating is to always ask yourself:

• What are you adding up? (Volume? Chocolate?)
• How are you chopping? (Draw a line in the region!)
• What are the limits? (Inner limits: from one end of your line to the other; Outer limits: from the first such line to the last.)

A good problem-solving strategy is to always start by writing down what you know and what you want.

10/26/15

With apologies, some of the links given in the reading assignments were incorrectly labeled, but have now been corrected.

References to "the text" should have pointed to this version, and references to Chapter 3 should have been to Chapter 2.

10/23/15

The midterm will be Friday 10/30/15 in class. (I got this wrong in class today...)
We will start at 8:30 AM.

• The topics to be covered on the midterm are
  • multiple integration;
  • partial differentiation.
• The exam is closed book, and calculators may not be used.
• You may bring one 3″×5″ index card (both sides) of handwritten notes.
• Please write your exams in pencil or black ink (blue ink is OK).
• Please turn off all electronic devices, such as cell phones and alarms; this also includes personal music players.
• Wednesday's class will be devoted to review. Come prepared to ask questions!

10/16/15

By popular request, the answer to the second homework problem is $28\pi/15$.

Here's another problem you might want to try. Read through the section on center of mass, then determine the center of mass of a hemisphere of uniform (that is, constant) density.

10/15/15

A picture of your second solution to yesterday's cone problem has now been posted here.

10/14/15

A picture of your first solution to today's cone problem can be found here. My summary pictures showing the different ways to chop can be found here and here, and the list of integration questions you came up with can be found here.

(With apologies, the limits on $\theta$ were cut off from the picture in spherical coordinates; the upper limit is $\tan^{-1}(R/H)$. The equation for the top of the cone is also missing, and should be $z=H=r\cos\theta$.)

10/12/15

You can find more information about the computation of $dV$ in spherical coordinates in §1.12, of the online text.

Expressions for $dV$ in both cylindrical and spherical coordinates can be found in §1.16.

You can find out more about the reasons we will use the "physics" convention for the names of the spherical coordinates in our paper:

Spherical Coordinates, Tevian Dray and Corinne A. Manogue, College Math. J. 34, 168–169 (2003)

The short answer is that most students will need to switch conventions at some point during their education, so this might as well be done sooner rather than later.

10/9/15

Yes, you should know how to use trig substitutions to evaluate integrals.

The most common substitutions are $x=a\sin\theta$ to simplify $\sqrt{a^2-x^2}$, and $x=a\tan\theta$ to simplify $\sqrt{a^2+x^2}$.

You should also be comfortable with the basic trig identities:

$\sin^2\theta+\cos^2\theta=1$
$\sin2\theta=2\sin\theta\cos\theta$
$\cos2\theta=\cos^2\theta-\sin^2\theta=2\cos^2\theta-1=1-2\sin^2\theta$

The slide I showed in class today about integrals in 1, 2, and 3 dimensions can be found here.

10/8/15

The Mathematics Learning Center (MLC) provides drop-in help for all lower-division mathematics courses, although not everybody there is good at vector calculus. The MLC is located on the ground floor of Kidder Hall (Kidder 108), and is normally open M–F from 9 AM to 4 or 5 PM, from the second week of term through Dead Week (Week 10). Evening help is also available; see their website for details.

The MLC also has a computer lab with software you may find helpful for doing mathematics, including Maple, Mathematica, and Matlab.

10/7/15

We didn't quite get to triple integrals today...

You should read this section before attempting the second problem on the homework, but all you really need to know is that $dV=dx\,dy\,dz$. If you find yourself stuck on 2(a), try 2(b) first.

10/5/15

I will be giving an informal talk on Wednesday as part of a new "Math Chats" series in the math dept:

Math Chat: Putting differentials back into calculus
Tevian Dray
Wednesday, 10/7/15, 4 PM, Covl 221
The use of differentials in introductory calculus courses provides a unifying theme which leads to a coherent view of calculus. We show in particular how differentials can be used to determine the derivatives of trigonometric and exponential functions, without the need for limits, numerical estimates, solutions of differential equations, or integration. This talk will consist of a relatively short formal presentation, followed by ample time for discussion.

The talk will definitely be accessible to students in this class, so please do come if you are interested.

10/2/15

If you're wondering where I've been this week, you can follow these links to the slides from my talk this afternoon at this physics conference, and the slides from my talk tomorrow afternoon at this math conference.

9/30/15

Computational skill is acquired through practice. Since the assigned homework problems in this course emphasize conceptual reasoning, you are strongly encouraged to test your understanding by also solving traditional, computational problems. Here are some resources to assist you:

• If you have access to a copy of the Briggs/Cochran text used in other sections, a list of problems assigned in another section can be found here.
• Copies of this and several other calculus books are on reserve in the library.
• I particularly recommend the problems in the Hughes Hallett book, which contains both relatively routine Exercises, and conceptually challenging Problems.

When using these books, you will of course have to figure out which sections are relevant. Our schedule does list the corresponding sections in Briggs/Cochran.

9/29/15

Tomorrow morning's office hour is canceled

This week only, you may attend Corinne Manogue's office hours: WRF 3–4 PM in Wngr 493.

9/28/15

The slide I showed in class today about chocolate on a wafer can be found here.

The green lines conneting the dots in III, IV, and V, do not appear in this version.

You are encouraged to work through at least one, and preferably two, ways of chopping the cylinder in today's activity.

Make sure that you obtain the corect answer for the volume!
You do not need to turn this in, but feel free to do so if you would like feedback.

9/25/15

We will (briefly) discuss the Heater activity on Monday, so I encourage you to think about answering the questions, especially the first three and the last two.

9/23/15

My office hours have been posted on the course homepage.

If you are unable to make my posted office hours, the best alternative times to try to schedule an appointment are late Wednesday morning or Monday and Friday afternoons. I am occasionally available on Tuesdays, but only rarely on Thursdays.

A calendar showing my rough schedule can be found here, or by clicking on the calendar icon on the homepage>

9/18/15

Here are some suggestions for improving the presentation of your written work:

• Restate the problem in your own words.
• Use (mostly) complete sentences (with the math included as grammatically correct parts).
• Don't write a book — keep it short and sweet.
• Don't use scratch paper; use blue or black ink (or pencil).
• Don't use a multicolumn format.

The goal of your writeups should be to be able to understand them 5 years from now without any additional information.

Further information is available at the top of the homework page.
The criteria I will use to evaluate written work can be found here.

8/20/15

Make sure you read the note about textbooks, and take a look at the grading policy.

I reserve the right to make small changes to these rules.