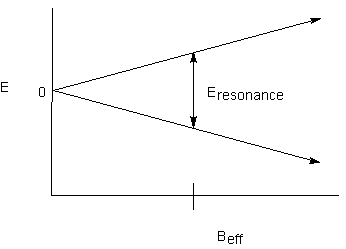
If there are two effective magnetic fields that the proton can experience, there will be two resonance energies:
The analysis of chemical shifts gives a lot of information about the number and type of electronic environments present in a molecule. However, an equally important tool for discovering organic structures lies in the analysis of coupling between nuclei. This facet of NMR spectroscopy allows us to establish the spatial relationship between atoms-literally drawing a map of the molecule!
Recall that each NMR-active nucleus has its own magnetic field as a result of its magnetic moment. Depending on the spin state of the nucleus, it will either add to or subtract from the external magnetic field. If the effect is large enough, any nucleus that can feel the magnetic effect of the first one will experience two different effective magnetic fields. Recall the relationship between energy levels and effective magnetic field:

If there are two effective magnetic fields that the proton can experience, there
will be two resonance energies:
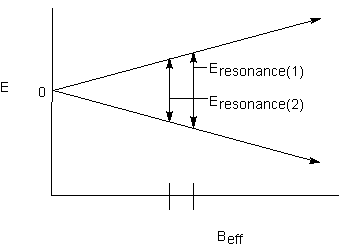
Finally, the effect of one nucleus on the other is commutative; both signals will be split into doublets by the other:
The energy difference between the two lines in a doublet is characteristic of the magnetic communication between the two nuclei. This is called the coupling constant; it has the designation J, is expressed in Hz, and is independent of the applied magnetic field.
If there are more than one equivalent nuclei, their effect is additive; for two spins, the spins can both add to or both subtract from the external field, or they can cancel each other. This leads to 3 magnetic environments for the coupled nucleus, and because of statistical probability, the triplet has an intensity ratio of 1:2:1.
Note here that the more intense downfield signal arises from two nuclei, coupled to the single upfield nucleus. The triplet arises from the single unique nucleus which experiences splitting by the two downfield nuclei.
It is important to keep straight two separate pieces of information:
A nucleus may, of course, be coupled to more than two nuclei, and the splitting pattern expected (if all coupling constants are equal) varies as described by Pascal's triangle:
| Coupled nuclei | Intensities | Pattern | ||||||
| 0 | 1 | Singlet (s) | ||||||
| 1 | 1 | 1 | Doublet (d) | |||||
| 2 | 1 | 2 | 1 | Triplet (t) | ||||
| 3 | 1 | 3 | 3 | 1 | Quartet (q) | |||
| 4 | 1 | 4 | 6 | 4 | 1 | Pentet (p) | ||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | Sextet | |
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | Septet |
Often the outside peaks of a multiplet are very small. Look at the 1H
spectrum of isopropyl iodide:
The blowup of the methine (CH) group shows that it is a heptet, as expected, but the two outer peaks are very small.
We need to consider two more effects before jumping into spectrum interpretation.
It need not be the case that all coupling a particular nucleus sees will carry the same coupling constant to every other nucleus. A proton may have a large coupling to one proton, and a small coupling to another.
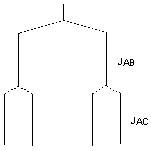
If we call the nuclei A, B and C in order, JAB equals JBC, so B is a triplet. But JAB ≠ JAC; look at an expansion of peak A. The two different couplings result in a doublet of doublets. The large splitting to nucleus B gives two lines, each of which is split by the small coupling to nucleus C:
 |
A final effect you need to be aware of is non-first-order behavior. In brief, as the difference in chemical shift decreases to the magnitude of the coupling constant, asymmetry appears (among other effects). Observe what happens when all that changes is a change in relative chemical shift:
Note that as the two chemical shifts get nearer, the outside signals become weaker than the inside signals. The ultimate case is the last; if the shifts are essentially the same, the outside peaks disappear and we see a singlet.