You are here: start » courses » lecture » cflec » cfleceffpotential
Energy and Effective Potential Lecture (25 minutes)
Central Forces Notes Sections 11 and 12
- The class begins with a review of 1-D potential energy diagrams using the harmonic oscillator as the key example. In preparation for the discussion of effective potential, time is spent discussing classical turning points.
- The energy expression for the central force problem is derived by substituting in an expression for the velocity in polar coordinates. $$E=\frac{1}{2} \mu \dot v^2 + U(r) \rightarrow E=\frac{1}{2} \mu \dot r^2 +\frac{1}{2} \frac{l^2}{mu r^2} + U(r) $$
- A discussion of the form for $U(r)$ can be very productive. In particular, it is useful to reason out the form of the potential energy, reminding students that the expression for the gravitational potential energy is $U= - \frac{1}{2} \frac{G m_1 m_2}{r}$ rather than $U=m g h$ (as they commonly recall). A discussion, reasoning out what sign $U(r)$ must have can also be very productive.
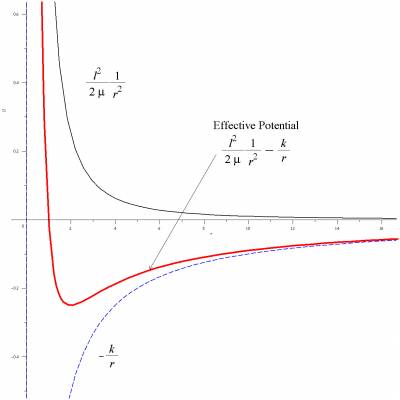
- The expressions for the total energy in the harmonic oscillator and the central force problem are written side-by-side $$E=\frac{1}{2} \mu \dot v^2 + \frac{1}{2} k x^2 \quad \quad \quad E=\frac{1}{2} \mu \dot r^2 +\frac{1}{2} \frac{l^2}{mu r^2} - \frac{k}{r}$$to elicit the connection between the harmonic oscillator potential energy, $\frac{1}{2} k x^2$, and the central force effective potential, $\frac{1}{2} \frac{l^2}{mu r^2} - \frac{k}{r}$
- After defining the effective potential and plotting $-\frac{1}{r}$ and $\frac{1}{r^2}$, students are asked to draw a graph of $-\frac{1}{r} + \frac{1}{r^2}$ as a small whiteboard question. This question leads to a good discussion of what this function will look like. Some useful questions for leading this discussion include:
- Is there a value of r for which the two terms cancel?
- What is the sign of the sum of the two terms for values of r less than this value?
- What is the sign of the sum of the two terms for values of r greater than this value?
- What happens to the sum for very large values of r?
- We relate the idea of the effective potential and the angular momentum barrier (due to conservation of angular momentum). In particular, it is useful to discuss what happens to the different parts of the energy equation when the orbiting body reaches its closest approach.
- After generating a plot similar to the one below, we begin the kinesthetic activity Interpreting Effective Potential Plots