A Review of Vector Calculus
The basic objects in vector calculus are vector fields $\FF$ in 3-dimensional Euclidean space, $\RR^3$. A vector field can be expressed in terms of a basis by giving its components with respect to that basis, such as 1) \begin{equation} \FF = F_x\,\xhat + F_y\,\yhat + F_z\,\zhat \end{equation} where $\{\xhat,\yhat,\zhat\}$ denotes the standard rectangular basis for $\RR^3$, also written as $\{\ii,\jj,\kk\}$.
Integration
One of the two fundamental operations in calculus is integration. In vector calculus, we are interested in integrating vector fields, and can do so over a curve $C$, \begin{equation} \int_C \FF\cdot d\rr \end{equation} which might represent the work done by the force $\FF$ when moving an object along the path $C$, or over a surface $S$, \begin{equation} \int_S \FF\cdot d\AA \end{equation} which might represent the flux of $\FF$ through $S$. Expressions for $d\rr$ in various coordinate systems can be computed explicitly by considering infinitesimal vector displacements; in rectangular coordinates, we have \begin{equation} d\rr = dx\,\xhat + dy\,\yhat + dz\,\zhat \end{equation}
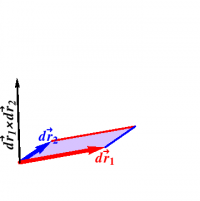
Similarly, coordinate expressions for $d\AA$ can be computed by chopping up the surface into infinitesimal parallelograms, whose (directed) areas are just the cross product of their sides, so that $d\AA$ can be expressed in the form \begin{equation} d\AA = d\rr_1 \times d\rr_2 \end{equation} as shown in Figure 1.
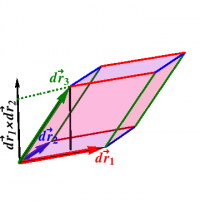
Vector calculus also involves the integration of functions over a region $R$, \begin{equation} \int_R f\,dV \end{equation} which might represent the total amount of chocolate in $R$ if $f$ gives the density of chocolate. The volume element can be determined by chopping up the region into infinitesimal parallelepipeds, whose volumes can be found using the triple product, leading to an expression of the form \begin{equation} dV = d\rr_1 \times d\rr_2 \cdot d\rr_3 \end{equation} as shown in Figure 2. Finally, we can evaluate functions at a point $P$, and we extend the ordinary notions of integration to include this case by defining \begin{equation} \int_P f = f\Big|_P \end{equation}
Thus, we can integrate over $0$-, $1$-, $2$-, or $3$-dimensional regions.
Differentiation
The other fundamental operation in calculus is differentiation. Much of vector calculus involves vector derivative operators, namely the gradient of a function $(\grad f)$, the curl of a vector field $(\grad\times\FF)$, and the divergence of a vector field $(\grad\cdot\FF)$. In rectangular coordinates, these operations are given by \begin{align} \grad f &= \Partial{f}{x}\,\xhat + \Partial{f}{y}\,\yhat + \Partial{f}{z}\,\zhat \\ \grad\times\FF &= \left| \begin{matrix}\xhat& \yhat& \zhat\\ \noalign{\smallskip} \Partial{}{x}& \Partial{}{y}& \Partial{}{z}\\ \noalign{\smallskip} F_x & F_y & F_z\\\end{matrix} \right| \\ \grad\cdot\FF &= \Partial{F_x}{x} + \Partial{F_y}{y} + \Partial{F_z}{z} \end{align} and satisfy the identities \begin{align} \grad\times\grad f &= \zero \label{curlgrad}\\ \grad\cdot\left(\grad\times\FF\right) &= 0 \label{divcurl} \end{align}
Theorems
Each of the above derivative operations leads to a version of the fundamental theorem of calculus. Integrating a gradient along a curve $C$ from point $A$ to point $B$ results in \begin{equation} \int_C \grad f\cdot d\rr = f\Big|_A^B \end{equation} which could be called the fundamental theorem for gradient. Integrating a curl over a surface $S$ with boundary $C$ leads to \begin{equation} \int_S \left(\grad\times\FF\right)\cdot d\AA = \oint_C \FF\cdot d\rr \end{equation} (with appropriate orientations) which is Stokes' Theorem. Finally, integrating a divergence over a region $R$ with boundary $S$ leads to \begin{equation} \int_R \grad\cdot\FF \,dV = \oint_S \FF\cdot d\AA \end{equation} which is the Divergence Theorem, and which relates the divergence of $\FF$ inside $S$ to the flux of $\FF$ out of $S$.