Integration Review Answers and Hints

As the title suggests, what follows are the answers to the integration practice problems on the Integration Review page. Where convenient, hints are given as to what procedure was used to obtain the answer. See the Review of Integration Techniques page for a short integration table and help with the different techniques of integration.

1. 
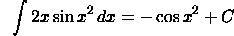
   Use the substitution u(x)=x^2.
    
2. 
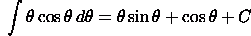
   Use integration by parts with u(x)=theta and v'(x)=cos(theta).
    
3. 
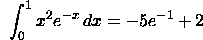
   Use integration by parts twice.
    
4. 
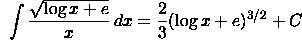
   Substitute u(x) for the function underneath the radical.
    
5. 
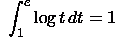
   Use integration by parts with u(t)=log(t) and v'(t)=1.
    
6. 
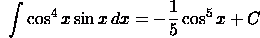
   Use the substitution u(x)=cos(x).
    

7. 
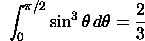
   Use the identity
    
   

8. 
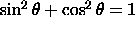
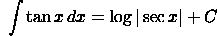
   Use the substitution u(x)=cos(x).
    
9. 
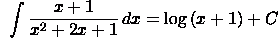
   Simplify algebraically and then integrate.
    
10. 
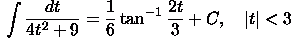
    See the table of integrals.
     
11. 
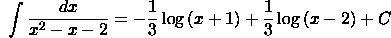
    Use the method of partial fractions. The partial fraction decomposition is
    
     
12. 
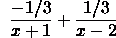
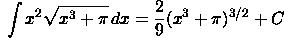
    Substitute u(x) for the function underneath the radical.
     
13. 
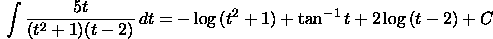
    Use the method of partial fractions. The partial fraction decomposition is
    

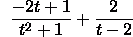
[Sequences and Series Home] [Vector Calculus Home] [Math 254 Home] [Math 255 Home] [ODE Home] [Notation]

Copyright © 1996 Department of Mathematics, Oregon State University

If you have questions or comments, don't hestitate to contact us.