Review of Integration Techniques

This page contains a review of some of the major techniques of integration, including

• Substitution methods
• Integration by Parts
• Integrating Rational Functions

and a table of common integrals. A more thorough and complete treatment of these methods can be found in your textbook (or any general calculus book). There is also a page of practice problems with answers which might be helpful.

Substitution

In some cases, an integral can be altered into a manageable form by just changing variables. If the integrand can be written in the form f(g(x))g'(x) then we may make the substitution u=g(x) (which implies du=g'(x)dx) and integrate as follows:

If the function f(u) has an easily indentifiable antiderivative then all is well. If not, another substitution or integration method may be needed. The common choices for g(x) are arguments of trigonometric functions and functions raised to powers.

Example

To evaluate the integral

we may consider choosing

u = 3 sin²(x) + e⁸
du = 6 sin(x) cos(x) dx

Then

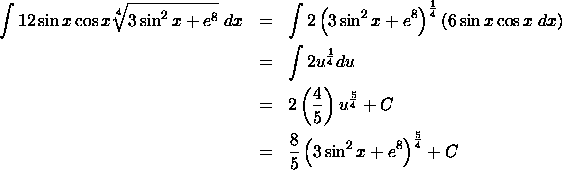
where C is a constant of integration.

Integration by Parts

Let u(x) and v(x) be two differentiable functions. An easy way to get the formula for integration by parts is as follows:

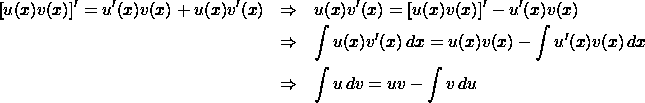
In the case of a definite integral we have

Integration by parts is useful in "eliminating" a part of the integral that makes the integral difficult to do. The annoying part of the integral is often chosen to be u(x).

Example

For the function

we notice that this function could be integrated with a substitution if the x^3 term were only an x. This is the perfect scenario for integration by parts. If we choose u(x)=x^2 and v'(x)=xe^(x^2), then we have

which implies

where C is a constant of integration.

Integrating Rational Functions

A rational function is a function that can be expressed as the ratio of two polynomials. Consider integrating the rational function

To integrate such a function we use the method of partial fractions to split the fraction into easily integrable pieces:

Now the integral is easy:

This method is designed for fractions with a polynomial of lesser degree in the numerator than in the denominator. If this is not the case, long (or synthetic) division must be carried out first and then the method of partial fractions can be used on the remainder term (if necessary).

Common Integrals

Below is a table of common integrals. Other integrals can be found in your textbook, a table of integrals and series, or any decent calculus book.

Copyright © 1996 Department of Mathematics, Oregon State University

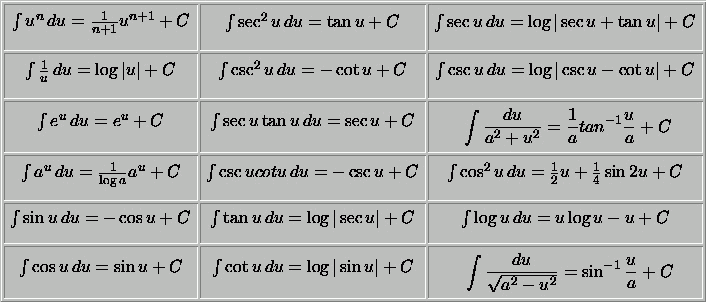
If you have questions or comments, don't hestitate to contact us.