A more modern approach is the molecular orbital theory. This also begins with the same set of atomic orbitals, but skips the step of hybridization.
You will remember from physical chemistry the simplest case, the H2 molecule. The description is actually indistinguishable from that generated from the valence bond approach, because hydrogen has only the 1s orbital available in the valence set.
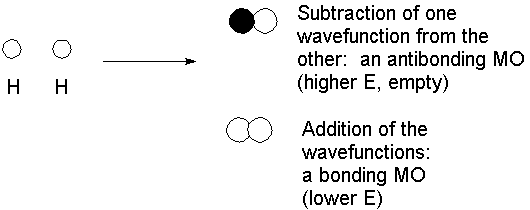
Interaction of 2 atomic orbitals gives 2 molecular orbitals. The 2 electrons are placed in the lowest energy MO. An empty "vitural" orbital exists as an out-of-phase combination; while it is irrelevant with regard to the bond, it can be used to explain spectroscopic features (e.g., σ-σ* excitation in the far UV).
The total energy of the molecule is minimized by allowing electrons to be delocalized over the entire molecule. The basics of the math can be found here.
Look at the orbitals calculated for the ethylene molecule:
|
These links are arranged in order of highest energy at the top, to lowest energy at the bottom.
Show the 12th MO; E>0.200 Show the 11th MO; E=+0.185 Show the 10th MO; E=+0.111 Show the 9th MO; E=+0.104 Show the 8th MO; E=+0.080 Show the 7th MO: the antibondi ng π*; E=+0.008 MO Show the 6th MO: the π MO; E=-0.274 Show the 5th MO; E=-0.353 Show the 4th MO; E=-0.420 Show the 3rd MO; E=-0.466 Show the 2nd MO; E=-0.578 Show the lowest energy MO; E=- 0.760 |
|
| Some of the molecular orbitals are recognizable in relation to the VB model (1 as the π bond, 3 as the C-C σ bond). The C-H σ bonds (2, 4, 5) are more delocalized, covering all hydrogens rather than individual C-H bonds. And there is always one completely in-phase bonding orbital covering all atoms (6). |
However, there are significant similarities between the two models. Each predicts the presence of electron density above and below the plane of the molecule (the π bond); this leads to restricted rotation about the C-C bond. Both models predict the substantial concentration of electron density between the atoms in σ bonds. A quantitative application of VB theory will, in fact, arrive at the same picture as the MO model, although doing so is more mathematically difficult. However, MO thoery is particularly good at describing aromatic systems, for which many resonance structures would be necessary for a full description.
Back to CH 630 Home page
Last updated: 05/04/2001