Next: Project
Up: Random Number Generators
Previous: Random Number Generators
The most common method of generating the random number sequence
 over
over 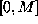 is known as the
linear congruent or power residue method. Multiply the previous
random number
is known as the
linear congruent or power residue method. Multiply the previous
random number  by the constant a, add on another constant
c, take the modulus by M, and then keep just the fractional
part (remainder) as the next random number
by the constant a, add on another constant
c, take the modulus by M, and then keep just the fractional
part (remainder) as the next random number 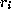 :
:

In (1), integer arithmetic is used to avoid round off error,
the value for  (the seed) is often supplied by the user,
and mod(n,m) is often a built-in function on your computer for
remaindering (it may be called amod, dmod).
(the seed) is often supplied by the user,
and mod(n,m) is often a built-in function on your computer for
remaindering (it may be called amod, dmod).
For example, if the subroutine has c=1, a=4, M=9 built in, and you
supply  , then you obtain the sequence:
, then you obtain the sequence:

Note that you obtain the same result for the mod operation by just
subtracting M until any further subtractions would leave a negative
number (what remains is the remainder).
The rule (1) produces integers in
the range  - but not necessarily every one. If a particular
integer comes up a second time, then the whole cycle repeats. In order
to obtain a long sequence and to have a rather random remainder, M
and a should be large numbers - but not so large that aM causes an
overflow.
- but not necessarily every one. If a particular
integer comes up a second time, then the whole cycle repeats. In order
to obtain a long sequence and to have a rather random remainder, M
and a should be large numbers - but not so large that aM causes an
overflow.
Your computer probably has a built in random number generator which
may well be better than the one you choose by chance. You should check
this out in the manual pages (try the man command) and then test
the generated sequence. These routines often have names like
rand, rn, random, srand, erand, or drand.
Here are two examples of how to call these routines in
C and
FORTRAN.
On the AIX system, the drand48 routine generates random numbers
in 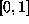 with good spectral properties. It uses
with good spectral properties. It uses
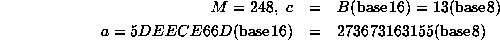
and 48 bit integer arithmetic. Make sure to initialize it properly by
calling the subroutine srand48 to plant your seed. To be safe,
you can reseed during your calculation (read manual for details).
The definition (1) will generate  's in the range
's in the range
 . If random numbers in the range
. If random numbers in the range 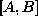 are needed, you need
only scale, for example:
are needed, you need
only scale, for example:

Here too, floating point numbers should be used to avoid
truncation.
Next: Project
Up: Random Number Generators
Previous: Random Number Generators
 over
over 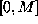 is known as the
linear congruent or power residue method. Multiply the previous
random number
is known as the
linear congruent or power residue method. Multiply the previous
random number  by the constant a, add on another constant
c, take the modulus by M, and then keep just the fractional
part (remainder) as the next random number
by the constant a, add on another constant
c, take the modulus by M, and then keep just the fractional
part (remainder) as the next random number 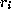 :
:

 (the seed) is often supplied by the user,
and mod(n,m) is often a built-in function on your computer for
remaindering (it may be called amod, dmod).
(the seed) is often supplied by the user,
and mod(n,m) is often a built-in function on your computer for
remaindering (it may be called amod, dmod).
 , then you obtain the sequence:
, then you obtain the sequence:

 - but not necessarily every one. If a particular
integer comes up a second time, then the whole cycle repeats. In order
to obtain a long sequence and to have a rather random remainder, M
and a should be large numbers - but not so large that aM causes an
overflow.
- but not necessarily every one. If a particular
integer comes up a second time, then the whole cycle repeats. In order
to obtain a long sequence and to have a rather random remainder, M
and a should be large numbers - but not so large that aM causes an
overflow.
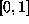 with good spectral properties. It uses
with good spectral properties. It uses
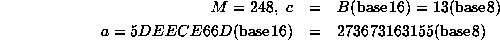
 's in the range
's in the range
 . If random numbers in the range
. If random numbers in the range 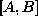 are needed, you need
only scale, for example:
are needed, you need
only scale, for example:
