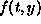near the midpoint
.
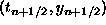As indicated earlier, the fourth order Runge-Kutta method is
generally considered to provide an excellent balance of power,
precision and simplicity to program. Here we use the first four terms of the
Taylor series to describe the behavior of 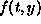near the midpoint
.
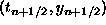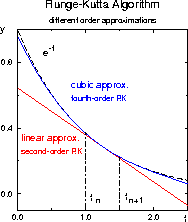
Figure 1.2: Runge-Kutta Algorithm
The fourth order Runge-Kutta requires four gradient or ''k'' terms to calculate
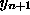
Note that the extra gradients can still be programmed simply with just four calls to the same subroutine.