The fourth order Runge-Kutta method is one of the standard (perhaps the standard) algorithm to solve differential equations. Before we give the algorithm of the fourth order Runge-Kutta method we will derive the second order Runge Kutta method.
We start with the original differential equation and integrate it formally.
We essentially changed the task at hand from performing a differentiation to an integration. To do this we expand f(t) in a second order Taylor series around the midpoint of the integration subinterval.
Yet since the integral of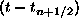 
vanishes when evaluated about the midpoint, we automatically get improved
precision using only the first term in (1).
This algorithm cannot be applied immediately since it requires a knowledge of
which is not in the scheme
of things. We thus approximate
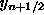with Euler's algorithm.
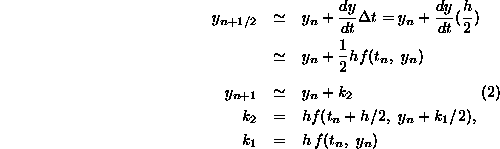
The second order Runge-Kutta algorithm (2) requires the known derivative function f at the endpoints and midpoint of the interval, and the unknown function y at the previous point. Since we start with initial conditions, the algorithm is self starting. Note too that it is applicable with a general function f (for example nonlinear), and simple to program.
